Um pequeno bloco de massa m1 está apoiado sobre outro bloco maior de massa
m2, e este, sobre um plano horizontal (ver figura ao lado). O bloco 1 é puxado com uma
força que forma um ângulo θ com a vertical e o bloco 2 é puxado na horizontal, o coeficiente de
atrito estático entre os blocos e entre o bloco e o plano são iguais a μ. Determinar os valores
mínimos das forças com que os blocos devem ser puxados para que o movimento comece, e, escrever os
vetores que representam estas forças.
Solução
Uma partícula de massa m é abandonada em repouso, cai sob ação do seu peso e sofre uma força de
resistência proporcional a velocidade de queda. Determinar:
a) A equação da velocidade em função do tempo;
b) A velocidade terminal;
c) A equação da posição em função do tempo;
d) A aceleração do movimento.
Solução
Uma partícula de massa m é lançada verticalmente para cima com velocidade inicial
v0 e sobe sob ação de uma força de resistência proporcional a velocidade. Determinar:
a) A equação da velocidade em função do tempo;
b) A equação da posição em função do tempo.
c) A altura máxima atingida pela partícula.
Solução
Um projétil de massa m é lançado com velocidade inicial v0 formando um ângulo
θ com a horizontal. O projétil sofre uma força de resistência devido ao ar proporcional a velocidade.
Determinar as equações da velocidade e posição em função do tempo.
Solução
Um corpo de massa m está preso a um fio inextensível, de massa desprezível e gira num plano
horizontal constituindo um pêndulo cônico. Sendo L o comprimento do fio e g a
aceleração local da gravidade, determine a velocidade tangencial que o corpo deve ter para que o ângulo
θ que o fio forma com a vertical seja 90°.
Solução
Um corpo de massa m está suspenso por um fio, inextensível e de massa desprezível, na ponta de um
suporte em forma de L invertido verticalmente, com a barra horizontal medindo D, conforme
figura. Este conjunto gira em torno do eixo vertical do suporte. Sendo L o comprimento do fio e
g a aceleração local da gravidade, determine a velocidade angular com que o conjunto deve girar
para que o ângulo θ que o fio forma com a vertical seja 90°.
Solução
Uma haste tem seu movimento limitado à vertical (para cima e para baixo), esta haste está apoiada num
plano inclinado formado por uma cunha de um ângulo α que desliza livremente sobre uma superfície
horizontal, conforme figura ao lado. A razão entre a massa da cunha pela massa da haste é igual a
r. Determinar as acelerações da haste e do plano inclinado. Desprezam-se todos os atritos.
Solução
Um sistema é formado por um corpo de massa m1, suspenso verticalmente, ligado a um
corpo de massa m2, apoiado sobre um plano inclinado de um ângulo α, que por sua
vez está ligado a um corpo de massa m3, apoiado sobre um plano inclinado de um ângulo
β. A ligação entre os corpos é feita por cordas inextensíveis de massas desprezíveis e através de
polias ideais sem atrito. Sabendo que m1 = 2 m2, pergunta-se, qual
deve ser a razão das massas m2 para m3 de tal modo que o sistema
desça com aceleração constante a.
Solução
No sistema da figura são conhecidas as massas m1 e m2. Calcule o
ângulo θ e as tensões nas cordas para que o sistema permaneça em equilíbrio. Despreze a massa da
roldana e os atritos.
Solução
Um bloco de 5 kg está sob a ação de uma força variável em função do tempo dada por
\[
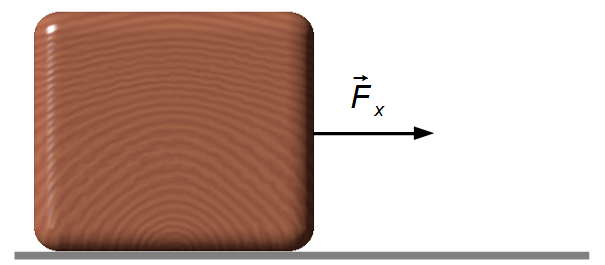
\begin{gather}
\qquad\qquad\qquad F_x=5t+2 \qquad\qquad\qquad \text{unidades (S.I.)}
\end{gather}
\]
sem outras forças atuando na direção
x. A velocidade inicial do bloco é igual à 0,5 m/s.
a) Qual a aceleração do bloco em
t = 2 s?
b) Qual a velocidade do bloco em
t = 5 s?
c) Qual o deslocamento do bloco entre
t = 2 e
t = 4 s?
Solução
Um corpo, de massa igual à 2 kg com velocidade inicial de 10 m/s no sentido positivo, está sob a ação
de uma força variável em função do tempo dada por
\[
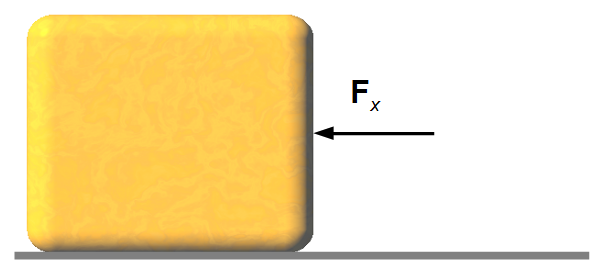
\begin{gather}
F_x=-8x \qquad\qquad\text{unidades (S.I.)}
\end{gather}
\]
Qual será a distância percorrida por esse corpo até que sua velocidade seja igual à zero?
Solução 1
Solução 2
Solução 3
Relação entre a Solução 2 e a Solução 3
EN
ES
FR
