Exercício Resolvido de Dinâmica
publicidade
Um corpo, de massa igual à 2 kg com velocidade inicial de 10 m/s no sentido positivo, está sob a ação
de uma força variável em função da posição, dada por
\[
\begin{gather}
F_x=-8x \qquad\qquad\text{unidades (S.I.)}
\end{gather}
\]
Qual será a distância percorrida por esse corpo até que sua velocidade seja igual à zero?
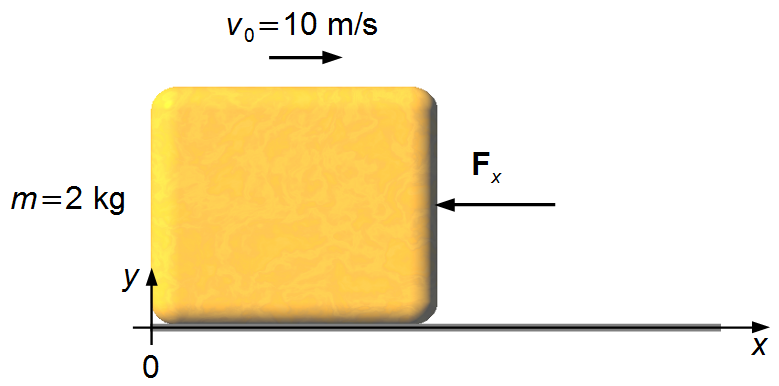
Dados do problema:
- Massa do corpo: m = 2 kg;
- Velocidade inicial do corpo: v0 = 10.
Adotamos um sistema de referência com eixo-x orientado para a direita e eixo-y para cima (Figura 1).
A força dada é negativa, é uma força de resistência que está na direção oposta do movimento. A força atua diminuindo a velocidade do corpo até que sua velocidade final seja igual a zero.
As Condições Iniciais são
\[
\begin{align}
& x(0)=0\\[10pt]
& v_{0}=\frac{dx(0)}{dt}=10\;\mathrm{m/s}
\end{align}
\]
Solução:
Aplicando a 2.ª Lei de Newton na direção x, a força dada no problema é a única força nesta direção
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf F=m\frac{d^2\mathbf x}{dt^2}}
\end{gather}
\]
\[
\begin{gather}
F_x=m\frac{d^2x}{dt^2}\\[5pt]
-8x=2\frac{d^2x}{dt^{2}}\\[5pt]
\frac{d^2x}{dt^2}+4x=0
\end{gather}
\]
Solução de
\( \displaystyle \frac{d^2x}{dt^2}+4x=0 \)
A solução deste tipo de equação é encontrada fazendo-se as substituições
A solução deste tipo de equação é encontrada fazendo-se as substituições
\[
\begin{align}
& x=\operatorname{e}^{\lambda t}\\[10pt]
& \frac{dx}{dt}=\lambda \operatorname{e}^{\lambda t}\\[10pt]
& \frac{d^2x\theta}{dt^2}=\lambda^2\operatorname{e}^{\lambda t}
\end{align}
\]
substituindo estes valores na equação diferencial
\[
\begin{gather}
\lambda^2\operatorname{e}^{\lambda t}+4\operatorname{e}^{\lambda t}=0\\[5pt]
\operatorname{e}^{\lambda t}\left(\lambda ^2+4\right)0\\[5pt]
\lambda^2+4=\frac{0}{\operatorname{e}^{\lambda t}}\\[5pt]
\lambda^2+4=0
\end{gather}
\]
esta é a Equação Característica que tem como solução
\[
\begin{gather}
\lambda_{1,2}=\pm\sqrt{-4\;}\\[5pt]
\lambda_{1,2}=\pm2\mathrm{i}
\end{gather}
\]
A solução da equação diferencial será
\[
\begin{gather}
x=C_1\operatorname{e}^{\lambda_1 t}+C_2\operatorname{e}^{\lambda_2 t}\\[5pt]
x=C_1\operatorname{e}^{2\mathrm{i}t}+C_{2}\operatorname{e}^{-2\mathrm{i}t}
\end{gather}
\]
onde C1 e C2 são constantes de integração, usando a
Fórmula de Euler
\( \operatorname{e}^{\mathrm{i}\theta}=\cos\theta+\mathrm{i}\operatorname{sen}\theta \)
\[
\begin{gather}
x=C_1\left(\cos2t+\mathrm{i}\operatorname{sen}2t\right)+C_{2}\left(\cos2t-\mathrm{i}\operatorname{sen}2t\right)\\[5pt]
x=C_1\cos2t+\mathrm{i}C_1\operatorname{sen}2t+C_2\cos2t-\mathrm{i}C_2\operatorname{sen}2t\\[5pt]
x=\left(C_1+C_{2}\right)\cos2t+\mathrm{i}\left(C_1-C_{2}\right)\operatorname{sen}2t
\end{gather}
\]
definindo duas novas constantes α e β em termos de C1 e
C2
\[
\begin{gather}
\alpha\equiv C_1+C_2\\[5pt]
\mathrm{e}\\[5pt]
\beta\equiv\mathrm{i}(C_1-C_2)
\end{gather}
\]
\[
\begin{gather}
x=\alpha\cos 2t+\beta\operatorname{sen}2t \tag{I}
\end{gather}
\]
Derivando a equação (I) em relação ao tempo, a função x(t) é a soma de duas funções, a
derivada da soma é dada pela soma das derivadas
\[
\begin{gather}
(f+g)'=f'+g'
\end{gather}
\]
e as funções seno e cosseno são funções compostas, usando a Regra da Cadeia
\[
\begin{gather}
\frac{df[w(t)]}{dt}=\frac{df}{dw}\frac{dw}{dt}
\end{gather}
\]
com
\( f=\alpha\cos w \),
\( g=\beta\operatorname{sen}w \)
e
\( w=2t \)
\[
\begin{gather}
\frac{dx}{dt}=\frac{df}{dt}+\frac{dg}{dt} \tag{II}\\[5pt]
\frac{dx}{dt}=\frac{df}{dw}\frac{dw}{dt}+\frac{dg}{dw}\frac{dw}{dt}\\[5pt]
\frac{dx}{dt}=\frac{d\left(\alpha\cos w\right)}{dw}\frac{d\left(2t\right)}{dt}+\frac{d\left(\beta\operatorname{sen}w\right)}{dw}\frac{d\left(2t\right)}{dt}\\[5pt]
\frac{dx}{dt}=\left(-\alpha\operatorname{sen}w\right)(2)+\left(\beta\cos w\right)(2)\\[5pt]
\frac{dx}{dt}=-2ialpha\operatorname{sen}2t+2ibeta\cos2t\\[5pt]
\frac{dx}{dt}=2\left(-\alpha\operatorname{sen}2t+\beta\cos2t\right) \tag{III}
\end{gather}
\]
Substituindo as Condições Iniciais nas equações (I) e (III)
\[
\begin{gather}
x(0)=0=\alpha\cos 2\times0+\beta\operatorname{sen}2\times 0\\[5pt]
\alpha=0 \tag{IV}
\end{gather}
\]
\[
\begin{gather}
\frac{dx(0)}{dt}=10=2\left(-0\times\operatorname{sen}2\times 0+\beta\cos 2\times0\right)\\[5pt]
10=2\beta\\[5pt]
\beta=5 \tag{V}
\end{gather}
\]
substituindo as constantes (IV) e (V) na equação (I)
\[
\begin{gather}
x=0\cos 2t+5\operatorname{sen}2t
\end{gather}
\]
A equação de movimento é dada por
\[
\begin{gather}
x(t)=5\operatorname{sen}2t \tag{VI}
\end{gather}
\]
Para encontrarmos o intervalo de tempo para que a velocidade do corpo seja igual a zero derivamos a
equação (VI)
Derivada de
\( \displaystyle x(t)=5\operatorname{sen}2t \)
A função x(t) é uma função composta, usando a Regra da Cadeia dada em (II), e fazendo \( f=5\operatorname{sen}w \) e \( w=2t \)
A função x(t) é uma função composta, usando a Regra da Cadeia dada em (II), e fazendo \( f=5\operatorname{sen}w \) e \( w=2t \)
\[
\begin{gather}
\frac{dx}{dt}=\frac{df}{dw}\frac{dw}{dt}\\[5pt]v(t)=\frac{d\left(5\operatorname{sen}w\right)}{dw}\frac{d\left(2t\right)}{dt}\\[5pt]
v(t)=\left(5\cos w\right)(2)\\[5pt]
v(t)=2\times 5\cos 2t\\[5pt]
v(t)=10\cos 2t
\end{gather}
\]
A equação da velocidade é dada por
\[
\begin{gather}
v(t)=10\cos 2t
\end{gather}
\]
fazendo v(t) = 0
\[
\begin{gather}
0=10\cos 2t\\[5pt]
\cos 2t=0\\[5pt]
2t=\arccos0\\[5pt]
t=\frac{1}{2}\;\arccos 0
\end{gather}
\]
Valores cujo o arco cosseno é zero (arccos 0)
\[
\begin{gather}
\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},...,\frac{(2n+1)\pi}{2},...\qquad\qquad n=0,1,2,3,...
\end{gather}
\]
Usando o primeiro valor para o qual o arco cosseno é zero \( \left(\frac{\pi}{2}\right) \), o intervalo de tempo para que a velocidade se anule será
\[
\begin{gather}
t=\frac{1}{2}\times{\frac{\pi}{2}}\\[5pt]
t=\frac{\pi}{4}\;\mathrm s
\end{gather}
\]
substituindo esse valor na equação (VI), a distância percorrida pelo corpo até parar será
\[
\begin{gather}
x\left(\frac{\pi}{4}\right)=5\operatorname{sen}2\times{\frac{\pi}{4}}\\[5pt]
x\left(\frac{\pi}{4}\right)=5\operatorname{sen}\frac{\pi }{2}
\end{gather}
\]
Da Trigonometria
\( \displaystyle \operatorname{sen}\frac{\pi}{2}=1 \)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x=5\;\mathrm m}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .