Exercício Resolvido de Dinâmica
publicidade
Um bloco de 5 kg está sob a ação de uma força variável em função do tempo dada por
a) Qual a aceleração do bloco em t = 2 s?
b) Qual a velocidade do bloco em t = 5 s?
c) Qual o deslocamento do bloco entre t = 2 e t = 4 s?
\[
\begin{gather}
\qquad\qquad\qquad F_x=5t+2 \qquad\qquad\qquad \text{unidades (S.I.)}
\end{gather}
\]
sem outras forças atuando na direção x. A velocidade inicial do bloco é igual à 0,5 m/s.a) Qual a aceleração do bloco em t = 2 s?
b) Qual a velocidade do bloco em t = 5 s?
c) Qual o deslocamento do bloco entre t = 2 e t = 4 s?
Dados do problema:
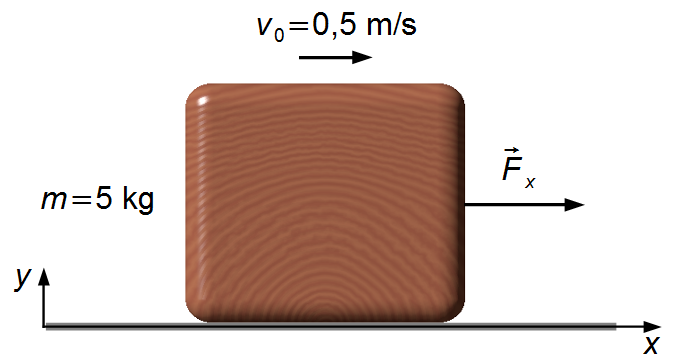
- Massa do bloco: m = 5 kg;
- Velocidade inicial do bloco: v0 = 0,5 m/s.
Adotamos um sistema de referência com eixo-x orientado para a direita e eixo-y para cima (Figura 1).
Solução:
a) Aplicando a 2.ª Lei de Newton na direção x, a força dada no problema é a única força nesta direção
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a}
\end{gather}
\]
\[
\begin{gather}
F_x=ma_x\\[5pt]
5t+2=5a_x\\[5pt]
a_x=\frac{5t+2}{5} \tag{I}
\end{gather}
\]
para t = 2 s
\[
\begin{gather}
a_x=\frac{5\times2+2}{5}\\[5pt]
a_x=\frac{12}{5}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_x=2,4\;\mathrm{m/s}^2}
\end{gather}
\]
b) A aceleração é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=\frac{dv}{dt}} \tag{II}
\end{gather}
\]
substituindo a fórmula (II) na equação (I) do item anterior
\[
\begin{gather}
\frac{dv_x}{dt}=\frac{5t+2}{5}\\[5pt]
\frac{dv_{x}}{dt}=t+0,4
\end{gather}
\]
integrando em dt de ambos os lados da igualdade
\[
\begin{gather}
\int\frac{dv_x}{dt}\;dt=\int t+0,4\;dt\\[5pt]
\int dv_x=\int t+0,4\;dt
\end{gather}
\]
do lado direito da igualdade, a integral da soma é igual à soma das integrais, e o fator constante 0,4 sai
da integral
\[
\begin{gather}
\int dv_x=\int t\;dt+0,4\int dt
\end{gather}
\]
Integral de \( \displaystyle \int dv_x \)
\[
\begin{gather}
\int 1\;dv_x=v_x+C_1
\end{gather}
\]
Integral de \( \displaystyle \int t\;dt \)
\[
\begin{gather}
\int t\;dt=\frac{t^{1+1}}{1+1}+C_1=\frac{t^2}{2}+C_1
\end{gather}
\]
Integral de \( \displaystyle \int dt \)
\[
\begin{gather}
\int 1\;dt=t+C_3
\end{gather}
\]
onde C1, C2 e C3 são constantes de integração
\[
\begin{gather}
v_x+C_{1}=\frac{t^2}{2}+C_1+0,4t+C_3\\[5pt]
v_x=\frac{t^2}{2}+0,4t+C_{3}+C_1-C_1
\end{gather}
\]
definindo as constantes C1, C2 e C3 como uma nova
constante C
\[
\begin{gather}
C\equiv C_3+C_1-C_1
\end{gather}
\]
A equação da velocidade é da forma
\[
\begin{gather}
v_x=\frac{t^2}{2}+0,4t+C
\end{gather}
\]
A constante C é determinada usando a condição inicial dada no problema, em t = 0, a
vx = 0,5 m/s
\[
\begin{gather}
v_x=\frac{t^{2}}{2}+0,4t+C\\[5pt]
0,5=\frac{0^2}{2}+0,4\times 0+C\\[5pt]
C=0,5\;\mathrm{m/s}
\end{gather}
\]
A equação da velocidade será
\[
\begin{gather}
v_x=\frac{t^2}{2}+0,4t+0,5 \tag{III}
\end{gather}
\]
para t = 5 s
\[
\begin{gather}
v_x=\frac{5^2}{2}+0,4\times 5+0,5\\[5pt]
v_x=\frac{25}{2}+2+0,5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_x=15\;\mathrm{m/s}}
\end{gather}
\]
c) A velocidade é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dx}{dt}} \tag{IV}
\end{gather}
\]
substituindo a fórmula (IV) na equação (III) do item anterior
\[
\begin{gather}
\frac{dx}{dt}=\frac{t^2}{2}+0,4t+0,5
\end{gather}
\]
integrando em dt de ambos os lados da igualdade
\[
\begin{gather}
\int\frac{dx}{dt}\;dt=\int\frac{t^2}{2}+0,4t+0,5\;dt\\[5pt]
\int dx=\int \frac{t^2}{2}+0,4t+0,5\;dt
\end{gather}
\]
do lado direito da igualdade, a integral da soma é igual à soma das integrais, e os fatores constantes
\( \frac{1}{2} \)
0,4 e 0,5 saem da integral
\[
\begin{gather}
\int dx=\frac{1}{2}\int t^2\;dt+0,4\int t\;dt+0,5\int dt
\end{gather}
\]
Integral de \( \displaystyle \int dx \)
\[
\begin{gather}
\int 1\;dx=x+C_4
\end{gather}
\]
Integral de \( \displaystyle \int t^2\;dt \)
\[
\begin{gather}
\int t^2\;dt=\frac{t^{2+1}}{2+1}+C_5=\frac{t^{3}}{3}+C_5
\end{gather}
\]
onde C4 e C5 são constantes de integração. As duas últimas integrais do lado direito da igualdade já foram calculadas acima
\[
\begin{gather}
x+C_4=\frac{1}{2}\times{\frac{t^{3}}{3}}+C_5+0,4\frac{t^2}{2}+C_6+0,5t+C_7\\[5pt]
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C_5+C_6+C_7-C_4
\end{gather}
\]
definindo as constantes C4, C5, C6 e
C7 como uma nova constante C'
\[
\begin{gather}
C'\equiv C_5+C_6+C_7-C_4
\end{gather}
\]
A equação da posição é da forma
\[
\begin{gather}
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C'
\end{gather}
\]
O problema não fornece a posição inicial do bloco, mas podemos determinar a constante C' fazendo a
suposição de que em t = 0, x = 0
\[
\begin{gather}
0=\frac{0^{3}}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'\\[5pt]
C'=0
\end{gather}
\]
A equação da posição será
\[
\begin{gather}
x=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t
\end{gather}
\]
para t = 2 s
\[
\begin{gather}
x_1=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2\\[5pt]
x_1=\frac{4}{3}+0,8+1\\[5pt]
x_1=3,1\;\mathrm m
\end{gather}
\]
para t = 4 s
\[
\begin{gather}
x_4=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4\\[5pt]
x_4=\frac{343}{6}+0,2\times49+3,5\\[5pt]
x_4=15,9\;\mathrm m
\end{gather}
\]
O deslocamento entre os instantes 2 s e 4 s, será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta x=x_f-x_i}
\end{gather}
\]
\[
\begin{gather}
\Delta x=x_4-x_1\\[5pt]
\Delta x=15,9-3,1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta x=12,8\;\mathrm m}
\end{gather}
\]
Observação: O que nos permite fazer a suposição de que em t = 0, temos x = 0?
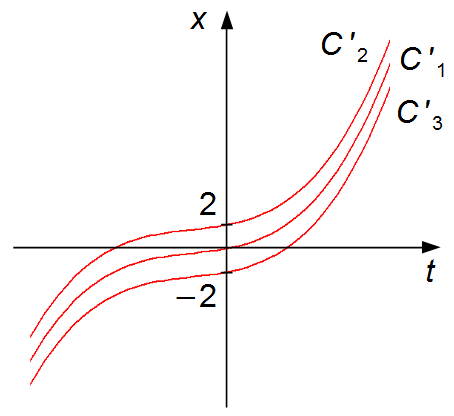 Gráfico 1
Gráfico 1
O eixo das abscissas representa o tempo t, como não existe tempo negativo, vamos construir o gráfico para valores do semieixo real positivo t.
Determinação de C' para diferentes valores de x e t:
 Gráfico 2
Gráfico 2
Calculando o valor de x(t) para t = 2 s e t = 4 s, usando vários valores de C'=0, 2, −2 (Gráfico 2).
Para dois outros instantes quaisquer escolhidos (por exemplo, 1 s e 7 s, ou 12 s e 23 s, ou 35 s e 100 s, etc) os deslocamentos serão diferentes de 12,8 m, porque o bloco está acelerado pela força aplicada. Mas os deslocamentos serão iguais entre esses instantes para as mesmas posições iniciais escolhidas.
Neste problema a posição é dada por uma função de 3.º grau
\[
\begin{gather}
x(t)=\frac{t^3}{6}+0,4\frac{t^2}{2}+0,5t+C'
\end{gather}
\]
o termo C', independente do tempo t, somente desloca o gráfico da função ao longo do
eixo-x (eixo das ordenadas - para cima e para baixo). Quanto maior o valor de C' o
gráfico se desloca na direção de x positivo (para cima). Quanto menor o valor de C' o
gráfico se desloca na direção de x negativo (para baixo) (Gráfico 1).

O eixo das abscissas representa o tempo t, como não existe tempo negativo, vamos construir o gráfico para valores do semieixo real positivo t.
Determinação de C' para diferentes valores de x e t:
-
Para t = 0 e x = 0
\( \displaystyle x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \)\[ x(0)=0=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_1\Rightarrow C'_1=0 \]; -
Para t = 0 e x = 2
\( \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \)\[ \displaystyle x(0)=2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times0+C'_1\Rightarrow C'_1=2 \]; -
Para t = 0 e x = −2
\( \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \)\[ \displaystyle x(0)=-2=\frac{0^3}{6}+0,4\times{\frac{0^2}{2}}+0,5\times 0+C'_3\Rightarrow C'_3=-2 \];

Calculando o valor de x(t) para t = 2 s e t = 4 s, usando vários valores de C'=0, 2, −2 (Gráfico 2).
-
Para C' = 0
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2=3,1\;\mathrm{m} \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4=15,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=15,9-3,1=12,8\;\mathrm m \]
-
Para C' = 2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times {\frac{2^2}{2}}+0,5\times 2+2=5,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+4\times 4+2=17,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=17,9-5,1=12,8\;\mathrm m \]
-
Para C' = −2
\( \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \)\[ \displaystyle x(2)=\frac{2^3}{6}+0,4\times{\frac{2^2}{2}}+0,5\times2-2=1,1\;\mathrm m \]
\( \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \)\[ \displaystyle x(4)=\frac{4^3}{6}+0,4\times{\frac{4^2}{2}}+0,5\times 4-2=13,9\;\mathrm m \]
\( \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \)\[ \displaystyle \Delta x=x(4)-x(2)=13,9-1,1=12,8\;\mathrm m \]
Para dois outros instantes quaisquer escolhidos (por exemplo, 1 s e 7 s, ou 12 s e 23 s, ou 35 s e 100 s, etc) os deslocamentos serão diferentes de 12,8 m, porque o bloco está acelerado pela força aplicada. Mas os deslocamentos serão iguais entre esses instantes para as mesmas posições iniciais escolhidas.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .