Exercício Resolvido de Dinâmica
publicidade
Um corpo, de massa igual à 2 kg com velocidade inicial de 10 m/s no sentido positivo, está sob a ação
de uma força variável em função da posição, dada por
\[
\begin{gather}
F_x=-8x \qquad\qquad\text{unidades (S.I.)}
\end{gather}
\]
Qual será a distância percorrida por esse corpo até que sua velocidade seja igual à zero?
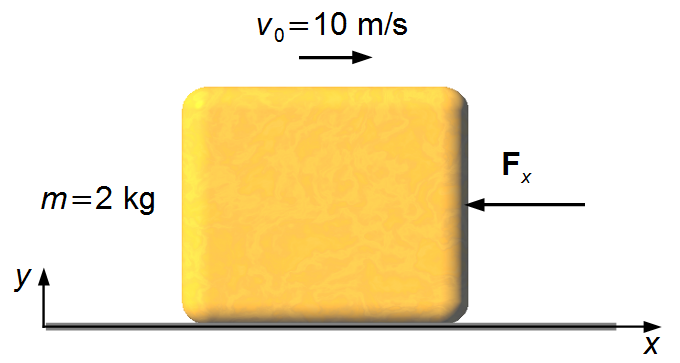
Dados do problema:
- Massa do corpo: m = 2 kg;
- Velocidade inicial do corpo: v0 = 10.
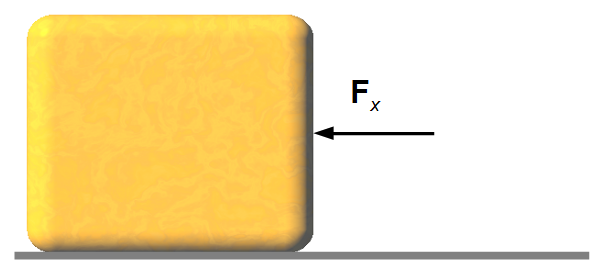
Adotamos um sistema de referência com eixo-x orientado para a direita e eixo-y para cima (Figura 1).
A força dada é negativa, é uma força de resistência que está na direção oposta do movimento. A força atua diminuindo a velocidade do corpo até que sua velocidade final seja igual a zero.
Solução:
Aplicando a 2.ª Lei de Newton na direção x, a força dada no problema é a única força nesta direção
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf F=m\frac{d\mathbf v}{dt}}
\end{gather}
\]
\[
\begin{gather}
F_x=m\frac{dv_x}{dt}\\[5pt]
-8x=2\frac{dv_x}{dt}
\end{gather}
\]
multiplicando e dividindo o lado direito da equação por dx
\[
\begin{gather}
-4x=\frac{dv_x}{dt}\frac{dx}{dx}
\end{gather}
\]
invertendo a ordem dos termos de integração no denominador
\[
\begin{gather}
-4x=\frac{dv_x}{dx}\frac{dx}{dt}
\end{gather}
\]
aplicando a definição da velocidade
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dx}{dt}}
\end{gather}
\]
integrando em dx de ambos os lados da igualdade
\[
\begin{gather}
\int -4x\;dx=\int v_x\frac{dv_x}{dx}\;dx\\[5pt]
\int-4x\;dx=\int v_x\;dv_x
\end{gather}
\]
o fator constante (−4) sai da integral do lado esquerdo
\[
\begin{gather}
-4\int x\;dx=\int v_x\;dv_x
\end{gather}
\]
Integral de
\( \displaystyle \int x\;dx \)
\[
\begin{gather}
\int x\;dx=\frac{x^{1+1}}{1+1}+C_1=\frac{x^2}{2}+C_1
\end{gather}
\]
Integral de
\( \displaystyle \int v_x\;dv_x \)
\[
\begin{gather}
\int v_x\;dv_x=\frac{v_x^{1+1}}{1+1}+C_2=\frac{v_x^2}{2}+C_2
\end{gather}
\]
onde C1 e C2 são constantes de integração.
\[
\begin{gather}
-4\left(\frac{x^2}{2}+C_1\right)=\frac{v_x^2}{2}+C_2\\[5pt]
-{\frac{4x^2}{2}}-4C_1=\frac{v_x^2}{2}+C_2\\[5pt]
-{\frac{4x^2}{2}}-4C_1-C_2=\frac{v_x^2}{2}
\end{gather}
\]
definindo as constantes C1 e C2 como uma nova constante C
\[
\begin{gather}
C\equiv -4C_1-C_2
\end{gather}
\]
A equação da velocidade em função da posição será da forma
\[
\begin{gather}
\frac{v_x^2}{2}=-{\frac{4x^2}{2}}+C
\end{gather}
\]
A constante C é determinada usando a condição inicial dada no problema, em x = 0, e
vx = 10 m/s
\[
\begin{gather}
\frac{10^2}{2}=-{\frac{4\times 0^2}{2}}+C\\[5pt]
C=\frac{100}{2}\\[5pt]
C=50
\end{gather}
\]
A equação da velocidade será
\[
\begin{gather}
\frac{v_x^2}{2}=-{\frac{4x^2}{2}}+50
\end{gather}
\]
multiplicando a equação por 2 de ambos os lados da igualdade
\[
\begin{gather}
\qquad\quad\quad \frac{v_x^2}{2}=-{\frac{4x^2}{2}}+50 \quad\quad \mathrm{(\times 2)} \\[5pt]
\frac{v_x^2}{\cancel 2}\times \cancel 2=-{\frac{4x^2}{\cancel 2}}\times \cancel 2+50\times 2 \\[5pt]
v_x^2=-4x^2+100
\end{gather}
\]
Quando a velocidade for igual a zero, vx = 0, a posição será
\[
\begin{gather}
0^2=-4x^2+100\\[5pt]
4x^2=100\\[5pt]
x=\sqrt{\frac{50}{2}\;}\\[5pt]
x=\sqrt{25\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x=5\;\mathrm m}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .