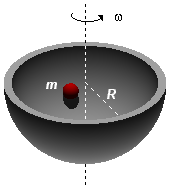
Uma pequena esfera de massa m é introduzida num recipiente cuja superfície interna é um hemisfério de raio R. Imprime-se ao recipiente em questão uma rotação em torno do eixo vertical com velocidade angular ω. Determinar:
a) A intensidade da força que a esfera faz contra a parede;
b) O raio da circunferência descrita pela esfera quando em equilíbrio em relação ao recipiente.

Numa haste cujo comprimento é L inclinada de um ângulo θ em relação à vertical, é enlaçado um anel que pode deslizar ao longo da mesma sem atrito. A haste é posta a girar, em torno de um eixo vertical que passa pela sua extremidade inferior com movimento uniforme. Determinar velocidade angular que deve ser efetuada pela haste para que o anel permaneça imóvel sobre a mesa no seu ponto médio.

Os corpos A e B têm massas 3m e 2m e deslizam sem atrito sobre o plano horizontal, o corpo C, pendurado na corda, tem massa m. Considere que a corda é inextensível e não tem massa, a roldana é de massa desprezível e sem atrito, e a aceleração da gravidade é g. Calcular as intensidades:
a) Da aceleração do corpo C;
b) Da reação de B sobre A.

O sistema esquematizado compõe-se de um elevador de massa M e um homem de massa m. O elevador está suspenso por uma corda que passa por uma polia fixa e vem às mãos do operador, a corda e a roldana são supostas ideais. O operador puxa a corda e sobe com aceleração constante a, juntamente com o elevador. São supostos conhecidos M, m, a e g. Determine a força que a plataforma exerce no operador.

Três corpos, A, B, e C estão suspensos, por cordas ideais, como representado na figura. O corpo B está suspenso simultaneamente por duas cordas, um ligado a A e outro a C. Determinar:
a) A aceleração e o sentido do movimento, se todas as massas são iguais a m;
b) A aceleração e o sentido do movimento, se as massas A e C são iguais a m e a massa B igual a 3m;
c) Se as massas A e C são iguais a m, qual deve ser o valor da massa B para que o movimento se dê para cima com aceleração igual a 0,5g?