Dinâmica
publicidade
Conceitos Básicos
Uma caixa de forma retangular, de massa m, está sobre uma superfície
horizontal. O coeficiente de atrito cinético é μ. Aplica-se uma força
\( \vec{F} \)
fazendo um ângulo α com a horizontal.
a) Para qual valor do ângulo α a aceleração da caixa é máxima?
b) Para quais valores de α a caixa permanece parada?
a) Para qual valor do ângulo α a aceleração da caixa é máxima?
b) Para quais valores de α a caixa permanece parada?

Planos Inclinados
Dois blocos, de massa mA e mB, são abandonados a
partir do repouso sobre planos inclinados muito longos. O bloco A está sobre um
plano que forma um ângulo α com a horizontal e o bloco B está sobre um
plano com ângulo β. Adote a aceleração da gravidade local igual a g e não
existe atrito entre os blocos e o plano inclinado. Determine a razão entre as
distâncias percorridas pelos blocos até que ambos possuam a mesma velocidade em módulo.
É dado um plano áspero inclinado de 45º em relação ao horizonte, do qual AB é
uma reta de maior declive. Um corpo é atirado no sentido ascendente, entra em repouso
em B retornando ao ponto A. O coeficiente de atrito entre o móvel e o
plano é
\( 2-\sqrt{3\;} \).
Determinar a relação entre o intervalo de tempo empregado pelo corpo para ir de
A até B e no retorno de B até A.
Um carrinho se desloca sobre uma superfície reta e horizontal. No carrinho há um
plano inclinado, que forma um ângulo θ com a horizontal, sobre o plano
coloca-se um corpo. Determinar a aceleração do carrinho para que o corpo permaneça
em repouso sobre o plano inclinado. Despreze o atrito entre o corpo e o plano
inclinado e adote g para a aceleração da gravidade.

Um carrinho se desloca sobre uma superfície reta e horizontal. No carrinho há um
plano inclinado, que forma um ângulo θ com a horizontal, sobre o plano
coloca-se um corpo, o coeficiente de atrito entre o corpo e o plano é μ.
Determinar a aceleração do carrinho para que o corpo esteja na iminência de subir
ao longo do plano. Adote g para a aceleração da gravidade.

Máquina de Atwood
Uma máquina de Atwood é disposta de tal maneira que as massas móveis
M1 e M2 ao invés de se moverem verticalmente,
são obrigadas a deslizar sem atrito sobre dois planos inclinados de 30º e 60º em
relação a horizontal. Supõe-se que as cordas que sustentam as massas
M1 e M2 são paralelos as retas de maior declive
desses planos. Determinar:
a) A relação entre M1 e M2 para que o sistema permaneça em equilíbrio;
b) Calcular a aceleração do movimento e a tensão na corda quando as massas são iguais, cada uma, a 5 kg.
Dada a aceleração da gravidade igual a 9,81 m/s2.
a) A relação entre M1 e M2 para que o sistema permaneça em equilíbrio;
b) Calcular a aceleração do movimento e a tensão na corda quando as massas são iguais, cada uma, a 5 kg.
Dada a aceleração da gravidade igual a 9,81 m/s2.

Um corpo de massa 12 kg está suspenso por um sistema de polias e cordas, como
mostrado na figura, um homem puxa a corda com uma força de 18 N. Supondo que estes
elementos são ideais, i.e., as polias não têm peso e não há atrito entre as
polias e as cordas e estes são inextensíveis e sem peso. Pergunta-se: o corpo irá
subir ou descer e com qual aceleração Adote para a aceleração da gravidade
g=10 m/s2.
Observação: i.e. é abreviação da expressão em latim id est, que significa isto é.

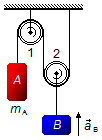
No sistema da figura, as polias 1 e 2 são ideais, a polia 1 é fixa e a polia 2 é
móvel. O bloco A possui massa 11 kg e o bloco B sobe com aceleração
1 m/s2. Determinar a aceleração do bloco A, a massa do bloco
B e a tensão na corda. Adote a aceleração da gravidade igual à
10 m/s2.
Uma corda passa por uma polia 1 fixa no teto, numa das extremidades existe um bloco
de massa mA = 36 kg, e na outra extremidade uma polia 2. Por esta
segunda polia passa uma corda em cujas extremidades se encontram corpos de massas
mB = 16 kg e mC = 8 kg (este sistema é uma
máquina de Atwood dupla). Calcular as acelerações das massas e as trações nas
cordas. As polias possuem massas e atrito desprezíveis, adote a aceleração da
gravidade igual a 10 m/s2.

Uma máquina de Atwood é formada por um bloco A, de massa igual a 100 kg, e um
bloco B, de massa igual à 300 kg, com o formato de um cubo de aresta igual a
0,60 m, imerso em um recipiente com água. Os blocos estão ligados por uma corda
inextensível e de massa desprezível que passa por uma polia sem atrito e também de
massa desprezível. Determine:
a) A aceleração do sistema;
b) A força de tensão na corda que liga as massas.
Adote a densidade da água igual a 1000 kg/m3 e a aceleração da gravidade igual a 10 m/s2.
a) A aceleração do sistema;
b) A força de tensão na corda que liga as massas.
Adote a densidade da água igual a 1000 kg/m3 e a aceleração da gravidade igual a 10 m/s2.

publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .