Determine a aceleração que o carrinho, mostrado na figura, deve ter para que o bloco não caia. Adote g para a aceleração da gravidade e μ para o coeficiente de atrito entre o bloco e o carrinho.

Um plano inclinado foi suspenso de modo que as massas m e M estão ligadas pelos dois lados por cordas A e B, conforme figura. Desprezando as massas das cordas e os atritos nas polias e sendo dados o ângulo de inclinação do plano igual a θ e a aceleração da gravidade g, determine:
a) A aceleração do conjunto, sabendo que a massa M está descendo o plano;
b) A diferença entre as tensões T_A e T_B.

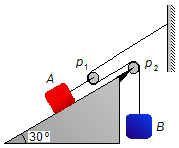
No sistema mostrado na figura, p₁ é uma polia móvel, p₂ uma polia fixa, o peso do bloco B é de 2 000 N e o ângulo do plano inclinado de 30°. Determinar qual deve ser o peso do bloco A para que o bloco B tenha uma velocidade de 20 m/s após um percurso de 40 m no sentido ascendente. Desprezam-se as massas das cordas e das polias e os atritos entre as cordas e as polias e entre o bloco B e o plano. Adote g = 10 m/s₂.

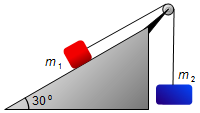
Sobre um plano inclinado de 30° em relação à horizontal, desliza sem atrito uma massa m₁ presa a uma outra massa m₂. Abandonando o sistema a partir do repouso a massa m₂ sobe 250 m em 20 s. Calcular a relação m₁/m₂. Adote g = 10 m/s².

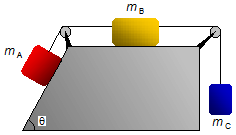
No sistema da figura, as massas de A, B e C valem respectivamente 10 kg, 20 kg e 5 kg e o sen θ = 0,8. Desprezando os atritos calcular a aceleração do conjunto e a intensidade das forças de tração nas cordas. Adotar g = 10 m/s².

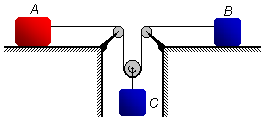
Na figura, o coeficiente de atrito entre os blocos A, B e os planos sobre os quais deslizam é 0,2. As massas de A, B e C valem respectivamente 100 kg, 50 kg e 50 kg. Determinar a aceleração de cada um dos blocos e a força que traciona a corda. Adote g = 10 m/s² e admita que 2a_C = a_A+a_B, onde a_A, a_B e a_C são, respectivamente, as acelerações dos blocos A, B e C. A corda e as polias são ideais.

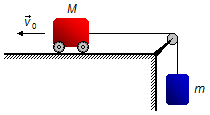
Um carrinho de massa M está unido por uma corda a uma carga de massa m. No momento inicial o carrinho tem velocidade v₀ e se move para a esquerda num plano horizontal. Determinar:
a) O intervalo de tempo decorrido até o carrinho parar;
b) O espaço percorrido até o carrinho parar.
Considere a corda inextensível e de massa desprezível, não existe atrito no plano horizontal e na polia e adote a aceleração da gravidade igual a g.

Que força horizontal deve ser constantemente aplicada a M = 21 kg para que m₁ = 5 kg não se movimente em relação a m₂ = 4 kg? Despreze o atrito e adote g = 10 m/s².