Circuitos RLC
publicidade
Oscilações em Circuitos RLC
a) Um circuito LC livre possui uma indutância L0 e uma capacitância
C0. Um outro circuito LC possui indutância L = nL0 e
capacitância C = nC0. Qual a razão das frequências das oscilações entre este
último e a frequência das oscilações do primeiro circuito?
b) Um circuito LC oscila com frequência f0, para uma indutância L0 e uma capacitância C0. Mantendo o mesmo valor de C0, substitui-se a bobina por outra de indutância L = nL0. Determine a nova frequência de ressonância.
b) Um circuito LC oscila com frequência f0, para uma indutância L0 e uma capacitância C0. Mantendo o mesmo valor de C0, substitui-se a bobina por outra de indutância L = nL0. Determine a nova frequência de ressonância.
Determinar o valor médio da energia elétrica, da energia magnética e da energia total de um circuito
LC com oscilações livres.
Mostre que o valor médio da tensão, aplicada a um elemento de um circuito, que tenha sua variação
proporcional ao seno ou cosseno é igual à zero. Mostre que o valor eficaz da tensão é igual à
\( \dfrac{\sqrt{2}}{2}V_{m} \),
onde Vm é o valor instantâneo máximo da tensão aplicada.
A corrente que passa em um circuito é dada por
a) A corrente média;
b) A corrente eficaz;
\[
\begin{gather}
i=2\operatorname{sen}4t
\end{gather}
\]
Determine:a) A corrente média;
b) A corrente eficaz;
Circuitos LC
Um circuito elétrico LC é composto por um indutor de 2 mH e um capacitor de 0,8 μF. A carga inicial do
capacitor é de 5 μC e a corrente no circuito é nula, determine:
a) A variação da carga no capacitor;
b) A variação da corrente no circuito;
c) Calcule a energia total armazenada no circuito;
d) O gráfico da variação da carga (q) em função do tempo (t). tempo t.
a) A variação da carga no capacitor;
b) A variação da corrente no circuito;
c) Calcule a energia total armazenada no circuito;
d) O gráfico da variação da carga (q) em função do tempo (t). tempo t.

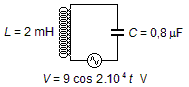
Um circuito elétrico LC é composto por um indutor de 2 mH e um capacitor de 0,8 μF e é alimentado por uma
fonte de tensão alternada V = 9 cos 2.104 t (volts). A carga inicial do capacitor é de
320 μC e a corrente no circuito é nula, determine:
a) A variação da carga no capacitor;
b) A variação da corrente no circuito.
a) A variação da carga no capacitor;
b) A variação da corrente no circuito.
Circuitos RLC
Para um circuito RLC em série, determine:
a) A equação para as oscilações dada pela carga em função do tempo q(t);
b) A solução da equação para o circuito no caso de amortecimento subcrítico, e a frequência angular das oscilações.
a) A equação para as oscilações dada pela carga em função do tempo q(t);
b) A solução da equação para o circuito no caso de amortecimento subcrítico, e a frequência angular das oscilações.

Um circuito RLC em série é formado por um resitor de resistência R = 75 Ω, um
indutor com indutância L = 10 mH e um capacitor de capacitância C = 0,20 μF. A carga
inicial armazenada no capacitor é igual a q0 = 0,4 mC e a corrente é nula.
Determine:
a) A equação da carga em função do tempo;
b) Classifique o tipo de oscilações desse circuito;
c) O gráfico da carga q em função do tempo t.
a) A equação da carga em função do tempo;
b) Classifique o tipo de oscilações desse circuito;
c) O gráfico da carga q em função do tempo t.

publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .