Exercício Resolvido de Circuitos RLC
publicidade
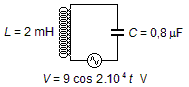
Um circuito elétrico LC é composto por um indutor de 2 mH e um capacitor de 0,8 μF e é
alimentado por uma fonte de tensão alternada V = 9 cos 2.104 t (volts). A carga
inicial do capacitor é de 320 μC e a corrente no circuito é nula, determine:
a) A variação da carga no capacitor;
b) A variação da corrente no circuito.
a) A variação da carga no capacitor;
b) A variação da corrente no circuito.
Dados do problema:
- Indutor: L = 2 mH = 2.10−3 H;;
- Capacitor: C = 0,8 μF = 8.10−7 F;
- f.e.m.: V = 9 cos 2.104 t (volts);
- Carga inicial no capacitor (t = 0): q0 = 320 μC = 3,2.10−4 C;
- Corrente inicial no circuito (t = 0): i0 = 0.
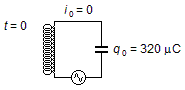
Admitimos que inicialmente o capacitor está carregado com carga máxima
(qmáx = q0) e a corrente no circuito é nula
(i0 = 0). A partir deste instante a fonte alimenta o circuito com uma uma corrente que
varia senoidalmente, a carga no capacitor diminui enquanto a corrente no circuito aumenta (Figura 1).
Com isto escrevemos as Condições Iniciais do problema:
\[
q(0)=3,2.10^{-4}\;\text{C}
\]
\[
i_{0}=\frac{dq(0)}{dt}=0
\]
Solução
a) Aplicando a Lei das Malhas de Kirchhoff (Figura 2)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum_{i=1}^{n}V_{i}=0} \tag{I}
\end{gather}
\]
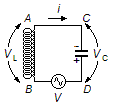
Figura 2
Entre os pontos A e B temos uma d.d.p. no indutor dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V_{L}=L\frac{di}{dt}} \tag{II}
\end{gather}
\]
e entre os pontos C e D a d.d.p. no capacitor é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V_{C}=\frac{q}{C}} \tag{III}
\end{gather}
\]
estas devem ser igual a f.e.m. fornecida pela fonte, substituindo as expressões (II) e (III)
na expressão (I)
\[
\begin{gather}
V_{L}+V_{C}-V=0\\
V_{L}+V_{C}=V\\
L\frac{di}{dt}+\frac{q}{C}=V
\end{gather}
\]
como corrente é a variação da carga no tempo,
\( i=\dfrac{dq}{dt} \)
\[
\begin{gather}
L\frac{d}{dt}\left(\frac{dq}{dt}\right)+\frac{q}{C}=V\\
L\frac{d^{2}q}{dt^{2}}+\frac{q}{C}=V
\end{gather}
\]
esta é uma Equação Diferencial Ordinária Não-Homogênea de 2.ª Ordem. Dividindo toda a equação
pela indutância L
\[
\frac{d^{2}q}{dt^{2}}+\frac{1}{LC}q=\frac{V}{L}
\]
substituindo os valores dados no problema
\[
\begin{gather}
\frac{d^{2}q}{dt^{2}}+\frac{1}{2.10^{-3}.8.10^{-7}}q=\frac{9}{2.10^{-3}}\cos 2.10^{4}t\\
\frac{d^{2}q}{dt^{2}}+\frac{1}{16.10^{-10}}q=4,5.10^{3}\cos 2.10^{4}t\\
\frac{d^{2}q}{dt^{2}}+\frac{1.10^{10}}{16}q=4,5.10^{3}\cos 2.10^{4}t\\
\frac{d^{2}q}{dt^{2}}+6,25.10^{8}q=4,5.10^{3}\cos 2.10^{4}t \tag{IV}
\end{gather}
\]
a solução desta equação será
\[
q=q_{h}+q_{p} \tag{V}
\]
onde qh é a solução da equação homogênea, igualando a zero, e qp é a
solução particular levando em consideração a função do lado direito da igualdade (no caso a f.e.m.
aplicada ao circuito).
- Solução da equação homogênea
\[
\frac{d^{2}q_{h}}{dt^{2}}+6,25.10^{8}q_{h}=0 \tag{VI}
\]
a solução deste tipo de equação é encontrada fazendo-se as substituições
\[
\begin{gather}
q_{h}=\operatorname{e}^{\lambda t}\\
\frac{dq_{h}}{dt}=\lambda\operatorname{e}^{\lambda t}\\
\frac{d^{2}q_{h}}{dt^{2}}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{gather}
\]
\[
\begin{gather}
\lambda ^{2}\operatorname{e}^{\lambda t}+6,25.10^{8}\operatorname{e}^{\lambda t}=0\\
\operatorname{e}^{\lambda t}\left(\lambda^{2}+6,25.10^{8}\right)=0\\
\lambda^{2}+6,25.10^{8}=\frac{0}{\operatorname{e}^{\lambda t}}\\
\lambda^{2}+6,25.10^{8}=0
\end{gather}
\]
esta é a Equação Característica que tem como solução
\[
\begin{gather}
\lambda ^{2}=-6,25.10^{8}\\
\lambda=\sqrt{-6,25.10^{8}\;}\\
\lambda_{1,2}=\pm 2,5.10^{4}\;\text{i}
\end{gather}
\]
onde
\( \text{i}=\sqrt{-1\;} \),
a solução da expressão (IV) é escrita como
\[
\begin{gather}
q_{h}=C_{1}\operatorname{e}^{\lambda_{1}t}+C_{2}\operatorname{e}^{\lambda_{2}t}\\
q_{h}=C_{1}\operatorname{e}^{2,5.10^{4}\;\operatorname{i}t}+C_{2}\operatorname{e}^{-2,5.10^{4}\;\operatorname{i}t}
\end{gather}
\]
onde C1 e C2 são constantes de integração, usando a
Relação de Euler (leia-se óiler)
\( \operatorname{e}^{\operatorname{i}\theta}=\cos \theta +\operatorname{i}\operatorname{sen}\theta \)
\[
\begin{gather}
q_{h}=C_{1}\left(\cos 2,5.10^{4}t+\operatorname{i}\operatorname{sen}2,5.10^{4}t\right)+C_{2}\left(\cos 2,5.10^{4}t-\operatorname{i}\operatorname{sen}2,5.10^{4}t\right)\\
q_{h}=C_{1}\cos 2,5.10^{4}t+\text{i}C_{1}\text{sen}2,5.10^{4}t+C_{2}\cos 2,5.10^{4}t-\text{i}C_{2}\text{sen}2,5.10^{4}t
\end{gather}
\]
coletando os termos em seno e cosseno
\[
\begin{gather}
q_{h}=\left(C_{1}+C_{2}\right)\cos 2,5.10^{4}t+\left(\text{i}C_{1}-\text{i}C_{2}\right)\text{sen}2,5.10^{4}t\\
q_{h}=\left(C_{1}+C_{2}\right)\cos 2,5.10^{4}t+\text{i}\left(C_{1}-C_{2}\right)\text{sen}2,5.10^{4}t
\end{gather}
\]
definindo duas novas constantes α e β em termos de C1 e C2
\[
\alpha \equiv C_{1}+C_{2}
\]
\[
\beta \equiv \text{i}(C_{1}-C_{2})
\]
\[
q_{h}=\alpha \cos 2,5.10^{4}t+\beta \text{sen}2,5.10^{4}t \tag{VII}
\]
multiplicando e dividindo esta expressão por
\( \sqrt{\alpha ^{2}+\beta ^{2}\;} \)
\[
\begin{gather}
q_{h}=\left(\alpha \cos 2,5.10^{4}t+\beta\text{sen}2,5.10^{4}t\right)\frac{\sqrt{\alpha ^{2}+\beta^{2}\;}}{\sqrt{\alpha ^{2}+\beta ^{2}\;}}\\
q_{h}=\sqrt{\alpha^{2}+\beta ^{2}\;}\left(\frac{\alpha }{\sqrt{\alpha ^{2}+\beta^{2}\;}}\cos 2,5.10^{4}t+\frac{\beta }{\sqrt{\alpha ^{2}+\beta^{2}\;}}\text{sen}2,5.10^{4}t\right)
\end{gather}
\]
fazendo as seguintes definições
\[
A\equiv \sqrt{\alpha ^{2}+\beta ^{2}\;}
\]
\[
\cos \varphi \equiv \frac{\alpha }{\sqrt{\alpha ^{2}+\beta ^{2}\;}}
\]
\[
\operatorname{sen}\varphi \equiv \frac{\beta }{\sqrt{\alpha ^{2}+\beta ^{2}\;}}
\]
temos
\[
q_{h}=A(\cos \varphi \cos 2,5.10^{4}t+\operatorname{sen}\varphi\operatorname{sen}2,5.10^{4}t)
\]
Observação: Lembrando da seguinte propriedade trigonométrica
\[
\cos (a-b)=\cos a\cos b+\operatorname{sen}a\operatorname{sen}b
\]
\[
\begin{gather}
q_{h}=A\cos (2,5.10^{4}t-\varphi ) \tag{VIII}
\end{gather}
\]
- Solução particular
\[
\frac{d^{2}q_{p}}{dt^{2}}+6,25.10^{8} q_{p}=4,5.10^{3} \cos\;2.10^{4}t \tag{IX}
\]
A solução deste tipo de equação é encontrada tomando-se a equação igual à função do lado direito da
igualdade. Como neste caso o lado direito é uma função cosseno, a solução particular deve ser uma função
formada por uma combinação de senos e cossenos, fazendo as seguintes substituições, onde
D1 e D2 são uma constante
\[
\begin{gather}
q_{p}=D_{1}\cos 2.10^{4}t+D_{2}\operatorname{sen}2.10^{4}t \tag{X}
\end{gather}
\]
- Derivada primeira de
\( q_{p}=D_{1}\cos 2.10^{4}t+D_{2}\operatorname{sen}2.10^{4}t \)
\( q_{p}=D_{1}\cos 2.10^{4}t+D_{2}\operatorname{sen}2.10^{4}t \)
\[
\frac{dq_{p}[u(t)+v(t)]}{dt}=\frac{dq_{1}}{du}\frac{du}{dt}+\frac{dq_{2}}{dv}\frac{dv}{dt}
\]
assim as derivadas serão
\[
\begin{array}{l}
q_{1}=D_{1}\cos u\\
\dfrac{dq_{1}}{du}=-D_{1}\operatorname{sen}u=-D_{1}\operatorname{sen}2.10^{4}t\\{}\\q_{2}=D_{2}\operatorname{sen}v\\
\dfrac{dq_{2}}{du}=D_{2}\cos v=D_{2}\cos 2.10^{4}t
\\{\,}\\
u(t)=v(t)=2.10^{4}t\\
\dfrac{du}{dt}=\dfrac{dv}{dt}=2.10^{4}
\end{array}
\]
\[
\frac{dq_{p}}{dt}=-2.10^{4}D_{1}\operatorname{sen}2.10^{4}t+2.10^{4}D_{2}\cos2.10^{4}t
\]
- Derivada segunda
\[
\begin{array}{l}
q_{3}=-2.10^{4}D_{1}\operatorname{sen}u\\
\dfrac{dq_{3}}{du}=-D_{1}\cos u=-D_{1}\cos 2.10^{4}t
\\{\,}\\
q_{4}=2.10^{4}D_{2}\cos v\\
\dfrac{dq_{4}}{du}=-2.10^{4}D_{2}\operatorname{sen}v=-2.10^{4}D_{2}\operatorname{sen}2.10^{4}t
\\{\,}\\
u(t)=v(t)=2.10^{4}t\\
\dfrac{du}{dt}=\dfrac{dv}{dt}=2.10^{4}
\end{array}
\]
\[
\begin{gather}
\frac{d^{2}q_{p}}{dt^{2}}=-2.10^{4}.2.10^{4}D_{1}\cos 2.10^{4}t-2.10^{4}.2.10^{4}D_{2}\operatorname{sen}2.10^{4}t\\
\frac{d^{2}q_{p}}{dt^{2}}=-4.10^{8}D_{1}\cos 2.10^{4}t-4.10^{8}D_{2}\operatorname{sen}2.10^{4}t \tag{XI}
\end{gather}
\]
substituindo as expressões (X) e (XI) na expressão (IX)
\[
\begin{array}{l}
-4.10^{8}D_{1}\cos 2.10^{4}t-4.10^{8}D_{2}\operatorname{sen}2.10^{4}t\text{+} \\
\qquad\qquad \text{+}6,25.10^{8}(D_{1}\cos 2.10^{4}t+D_{2}\operatorname{sen}2.10^{4}t)=4,5.10^{3}\cos 2.10^{4}t\\
-4.10^{8}D_{1}\cos 2.10^{4}t-4.10^{8}D_{2}\operatorname{sen}2.10^{4}t\text{+} \\
\qquad\qquad \text{+}6,25.10^{8}D_{1}\cos 2.10^{4}t+6,25.10^{8}D_{2}\operatorname{sen}2.10^{4}t=4,5.10^{3}\cos 2.10^{4}t\\
(-4.10^{8}D_{1}+6,25.10^{8}D_{1})\cos 2.10^{4}t+(-4.10^{8}D_{2}+6,25.10^{8}D_{2})\operatorname{sen}2.10^{4}t\text{=} \\
\qquad\qquad \text{=}4,5.10^{3}\cos 2.10^{4}t\\
2,15.10^{8}D_{1}\cos 2.10^{4}t+2,15.10^{8}D_{2}\operatorname{sen}2.10^{4}t=4,5.10^{3}\cos 2.10^{4}t+0.\operatorname{sen}2.10^{4}t
\end{array}
\]
igualando os coeficientes dos termos em seno e cosseno obtermos as constantes D1 e
D2
\[
\begin{gather}
2,15.10^{8}D_{1}=4,5.10^{3}\\
2,15.10^{8}D_{2}=0
\end{gather}
\]
da primeira expressão temos o valor de D1
\[
\begin{gather}
D_{1}=\frac{4,5.10^{3}}{2,15.10^{8}}\\
D_{1}=2.10^{-5}
\end{gather}
\]
da segunda expresão temos o valor de D2
\[
\begin{gather}
D_{2}=\frac{0}{2,15.10^{8}}\\
D_{2}=0
\end{gather}
\]
Assim a solução particular da expressão (X) será
\[
q_{p}=2.10^{-5}\cos 2.10^{4} t \tag{XII}
\]
substituindo as expressões (VIII) e (XII) na expressão (V)
\[
q=A\cos (2,5.10^{4}t-\varphi)+2.10^{-5}\cos 2.10^{4}t \tag{XIII}
\]
onde A e φ são constantes de integração determinadas pelas Condições Iniciais. Derivando a
expressão (XIII) em relação ao tempo
Derivada de
\( q=A\cos (2,5.10^{4}t-\varphi)+2.10^{-5}\cos 2.10^{4}t \)
cada um dos termos da função q(t) é uma função composta cuja derivada é dada pela Regra da Cadeia
\( q=A\cos (2,5.10^{4}t-\varphi)+2.10^{-5}\cos 2.10^{4}t \)
cada um dos termos da função q(t) é uma função composta cuja derivada é dada pela Regra da Cadeia
\[
\frac{dq[u(t)+v(t)]}{dt}=\frac{dq_{h}}{du}\frac{du}{dt}+\frac{dq_{p}}{dv}\frac{dv}{dt}
\]
assim as derivadas serão
\[
\begin{array}{l}
q_{h}=A\cos u\\
\dfrac{dq_{h}}{du}=-A\operatorname{sen}u=-A\operatorname{sen}(2,5.10^{4}t-\varphi)
\\{\,}\\
u(t)=2,5.10^{4}t-\varphi\\
\dfrac{du}{dt}=2,5.10^{4}
\\{\,}\\
q_{p}=2.10^{-5}\cos v\\
\dfrac{dq_{p}}{dv}=-2.10^{-5}\operatorname{sen}v=-2.10^{-5}\operatorname{sen}2.10^{4}t
\\{\,}\\
v(t)=2.10^{4}t\\
\dfrac{dv}{dt}=2.10^{4}
\end{array}
\]
\[
\begin{gather}
\frac{dq}{dt}=-2,5.10^{4}A\operatorname{sen}(2,5.10^{4}t-\varphi)-2.10^{-5}.2.10^{4}\operatorname{sen}2.10^{4}t\\
\frac{dq}{dt}=-2,5.10^{4}A\operatorname{sen}(2,5.10^{4}t-\varphi)-0,4\operatorname{sen}2.10^{4}t \tag{XIV}
\end{gather}
\]
Substituindo a Condição Inicial para q(0) na expressão (XIII)
\[
\begin{gather}
q(0)=3,2.10^{-4}=A\cos (2,5.10^{4}.0-\varphi)+2.10^{-5}\cos 2.10^{4}.0\\
3,2.10^{-4}=A\cos (-\varphi )+2.10^{-5}\cos 0
\end{gather}
\]
como o cosseno é uma função par temos
\( \cos \varphi =\cos (-\varphi) \)
e
\( \cos 0=1 \)
\[
\begin{gather}
3,2.10^{-4}-2.10^{-5}=A\cos \varphi \\
A\cos \varphi=3,2.10^{-4}-0,2.10^{-4}\\
A\cos \varphi =3.10^{-4} \tag{XV}
\end{gather}
\]
Substituindo a Condição Inicial para
\( \frac{dq(0)}{dt} \)
na expressão (XIV)
\[
\begin{gather}
\frac{dq(0)}{dt}=0=-2,5.10^{4}A\operatorname{sen}(2,5.10^{4}.0-\varphi)-0,4\operatorname{sen}2.10^{4}.0\\
0=-2,5.10^{4}A\operatorname{sen}(-\varphi)-0,4\operatorname{sen}0
\end{gather}
\]
como o seno é uma função ímpar
\( \operatorname{sen}\varphi =-\operatorname{sen}(-\varphi ) \)
e
\( \operatorname{sen}0=0 \)
\[
2,5.10^{4}A\operatorname{sen}\varphi =0 \tag{XVI}
\]
isolando o valor de A na expressão (XV)
\[
A=\frac{3.10^{-4}}{\cos \varphi } \tag{XVII}
\]
e substituindo em (XVI)
\[
\begin{gather}
2,5.10^{4}.\frac{3.10^{-4}}{\cos \varphi}.\operatorname{sen}\varphi =0\\
\operatorname{tg}\varphi =0\\
\varphi =\operatorname{arc tg}(0)\\
\varphi =0
\end{gather}
\]
substituindo o valor de φ em (XVII)
\[
\begin{gather}
A=\frac{3.10^{-4}}{\cos 0}\\
A=\frac{3.10^{-4}}{1}\\
A=3.10^{-4}
\end{gather}
\]
substituindo estas constantes na expressão (XIII)
\[ \bbox[#FFCCCC,10px]
{q(t)=3.10^{-4}\cos 2,5.10^{4}t+2.10^{-5}\cos 2.10^{4}t}
\]
b) A corrente será dada pela derivada da carga em função do tempo
\[
i=\frac{dq}{dt}
\]
a derivada é dada pela expressão (XIV), substituindo as constantes A e φ obtidas acima
\[
i(t)=-2,5.10^{4}.3.10^{-4}\operatorname{sen}(2,5.10^{4}t-0)-0,4\operatorname{sen}2.10^{4} t
\]
\[ \bbox[#FFCCCC,10px]
{i(t)=-7,5\operatorname{sen}2,5.10^{4}t-0,4\operatorname{sen}2.10^{4}t}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .