Esercizio Risolto di Forza Elettrica
pubblicità   

Due cariche elettriche puntiformi e positive, di cui una è il triplo dell’altra, si respingono con una forza di intensità pari a 2,7 N nel vuoto quando la distanza tra di esse è di 10 cm. Determina la minore delle cariche.
Costante di Coulomb nel vuoto:   \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

 

Dati del problema:

  • Carica 1:    q1 = Q;
  • Carica 2:    q2 = 3Q;
  • Forza elettrica di repulsione tra le cariche:    FE = 2,7 N;
  • Distanza tra le cariche:    d = 10 cm;
  • Costante di Coulomb nel vuoto:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

Schema del problema:

La forza FE12 è la forza di repulsione sulla sfera 1 dovuta alla sfera 2, mentre la forza FE21 è la forza di repulsione sulla sfera 2 dovuta alla sfera 1. I moduli di queste forze sono uguali a FE (Figura 1).

Figura 1

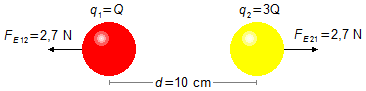
Soluzione:

Innanzitutto, dobbiamo convertire la distanza data in centimetri (cm) in metri (m), come richiesto dal Sistema Internazionale di Unità (SI).

\[ \begin{gather} d=10\;\mathrm{\cancel{cm}}\times\frac{1\;\mathrm m}{100\;\mathrm{\cancel{cm}}}=0,01\;\mathrm m=1\times10^{-2}\;\mathrm m \end{gather} \]

Applicando la Legge di Coulomb, il modulo della forza elettrica è dato da

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;q_1\;||\;q_2\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;Q\;||\;3Q\;|}{d^2} \\[5pt] 3Q^2=\frac{F_{\small E}d^2}{k_e} \\[5pt] Q=\sqrt{\frac{F_{\small E}d^2}{3k_e}} \\[5pt] Q=\sqrt{\frac{2,7\times 1\times 10^{-2}}{3\times 9\times 10^9}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=1\times 10^{-6}\;\mathrm C} \end{gather} \]
Osservazione: Se la carica minore vale q1 = 1×10−6 C, allora la carica maggiore vale q2 = 3×1×10−6 = 3×10−6 C.
pubblicità   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .