Gelöste Übung zur Elektrischen Kraft
Werbung   

Zwei punktförmige, positive elektrische Ladungen, von denen eine das Dreifache der anderen ist, stoßen sich im Vakuum mit einer Kraft von 2,7 N ab, wenn der Abstand zwischen ihnen 10 cm beträgt. Bestimme die kleinere der beiden Ladungen.
Coulomb-Konstante im Vakuum:   \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

 

Gegebene Daten:

  • Ladung 1:    q1 = Q;
  • Ladung 2:    q2 = 3Q;
  • Elektrische Abstoßungskraft zwischen den Ladungen:    FE = 2,7 N;
  • Abstand zwischen den Ladungen:    d = 10 cm;
  • Coulomb-Konstante im Vakuum:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

Schema des Problems:

Die Kraft FE12 ist die Abstoßungskraft auf Kugel 1 durch Kugel 2, die Kraft FE21 ist die Abstoßungskraft auf Kugel 2 durch Kugel 1. Der Betrag dieser Kräfte ist gleich FE (Abbildung 1).

Abb. 1

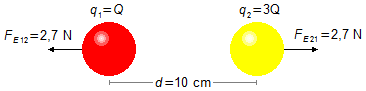
Lösung:

Zuerst muss der angegebene Abstand von Zentimetern (cm) in Meter (m) umgerechnet werden, wie es im Internationalen Einheitensystem (SI) verwendet wird.

\[ \begin{gather} d=10\;\mathrm{\cancel{cm}}\times\frac{1\;\mathrm m}{100\;\mathrm{\cancel{cm}}}=0,01\;\mathrm m=1\times10^{-2}\;\mathrm m \end{gather} \]

Anwendung des Coulomb-Gesetzes wird der Betrag der elektrischen Kraft gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;q_1\;||\;q_2\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;Q\;||\;3Q\;|}{d^2} \\[5pt] 3Q^2=\frac{F_{\small E}d^2}{k_e} \\[5pt] Q=\sqrt{\frac{F_{\small E}d^2}{3k_e}} \\[5pt] Q=\sqrt{\frac{2,7\times 1\times 10^{-2}}{3\times 9\times 10^9}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=1\times 10^{-6}\;\mathrm C} \end{gather} \]
Anmerkung: Wenn die kleinere Ladung q1 = 1×10−6 C beträgt, dann hat die größere den Wert q2 = 3×1×10−6 = 3×10−6 C.
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .