Ejercicio Resuelto sobre Fuerza Eléctrica
publicidad   

Dos cargas eléctricas puntuales positivas, de las cuales una es el triple de la otra, se repelen con una fuerza de módulo 2,7 N en el vacío cuando la distancia entre ellas es de 10 cm. Determine la menor de las cargas.
La Constante de Coulomb en el vacío es   \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

 

Datos del problema:

  • Carga 2:    q2 = 3Q;
  • Carga 1:    q1 = Q;
  • Fuerza eléctrica de repulsión entre las cargas:    FE = 2,7 N;
  • Distancia entre las cargas:    d = 10 cm;
  • Constante de Coulomb en el vacío:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

Esquema del problema:

La fuerza FE12 es la fuerza de repulsión sobre la esfera 1 debido a la esfera 2, la fuerza FE21 es la fuerza de repulsión sobre la esfera 2 debido a la esfera 1. En módulo, estas fuerzas son iguales a FE (Figura 1).

Figura 1

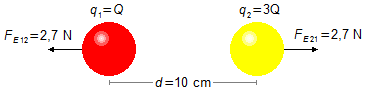
Solución:

Primero, debemos convertir la distancia dada de centímetro (cm) a metro (m) utilizado en el Sistema Internacional de Unidades (SI).

\[ \begin{gather} d=10\;\mathrm{\cancel{cm}}\times\frac{1\;\mathrm m}{100\;\mathrm{\cancel{cm}}}=0,01\;\mathrm m=1\times10^{-2}\;\mathrm m \end{gather} \]

Aplicando la Ley de Coulomb, el módulo de la fuerza eléctrica está dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;q_1\;||\;q_2\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;Q\;||\;3Q\;|}{d^2} \\[5pt] 3Q^2=\frac{F_{\small E}d^2}{k_e} \\[5pt] Q=\sqrt{\frac{F_{\small E}d^2}{3k_e}} \\[5pt] Q=\sqrt{\frac{2,7\times 1\times 10^{-2}}{3\times 9\times 10^9}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=1\times 10^{-6}\;\mathrm{C}} \end{gather} \]
Observación: Si la carga menor es q1 = 1×10−6 C, entonces la carga mayor es q2 = 3×1×10−6 = 3×10−6 C.
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .