Exercício Resolvido de Força Elétrica
publicidade   

Duas cargas elétricas positivas e puntiformes, das quais uma é o triplo da outra, repelem-se com força de intensidade 2,7 N no vácuo quando a distância entre elas é de 10 cm. Determine a menor das cargas.
Constante de Coulomb no vácuo   \( k_0=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

 

Dados do problema:

  • Carga 1:    q1 = Q;
  • Carga 2:    q2 = 3Q;
  • Força elétrica de repulsão entre as cargas:    FE = 2,7 N;
  • Distância entre as cargas:    d = 10 cm;
  • Constante de Coulomb no vácuo:    \( k_0=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

Esquema do problema:

A força FE12 é a força de repulsão sobre a esfera 1 devido à esfera 2, a força FE21 é a força de repulsão sobre a esfera 2 devido à esfera 1. O módulo estas forças são iguais à FE (Figura 1).

Figura 1

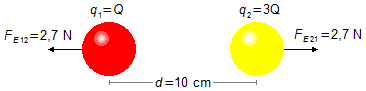
Solução:

Em primeiro lugar, devemos converter a distância dada em centímetro (cm) para metro (m) usado no Sistema Internacional de Unidades (S.I.).

\[ \begin{gather} d=10\;\mathrm{\cancel{cm}}\times\frac{1\;\mathrm m}{100\;\mathrm{\cancel{cm}}}=0,01\;\mathrm m=1\times10^{-2}\;\mathrm m \end{gather} \]

Aplicando a Lei de Coulomb, o módulo da força elétrica é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_0\frac{|\;q_1\;||\;q_2\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_0\frac{|\;Q\;||\;3Q\;|}{d^2} \\[5pt] 3Q^2=\frac{F_{\small E}d^2}{k_0} \\[5pt] Q=\sqrt{\frac{F_{\small E}d^2}{3k_0}} \\[5pt] Q=\sqrt{\frac{2,7\times 1\times 10^{-2}}{3\times 9\times 10^9}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=1\times 10^{-6}\;\mathrm C} \end{gather} \]
Observação: Se a carga menor vale q1 = 1×10−6 C, a carga maior vale q2 = 3×1×10−6 = 3×10−6 C.
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .