Solved Problem on Coulomb's Law
advertisement   



Two positive point charges, of which one is triple the other, repel with magnitude force 2.7 N in a vacuum when the distance between them is 10 cm. Determine the charge of the small value. Coulomb Constant in a vacuum   \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).


Problem data:
  • Charge 1:    q1 = Q;
  • Charge 2:    q2 = 3Q;
  • Electric force of repulsion between the charges:    FE = 2.7 N;
  • Distance between the charges:    d = 10 cm;
  • Coulomb Constant in a vacuum:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).
Problem diagram:

The force FE12 is the repulsion force on sphere 1 due to sphere 2, the force FE21 is the repulsion force on the sphere 2 due to sphere 1, the magnitude of these forces is equal to the FE (Figure 1).

>
Figure 1

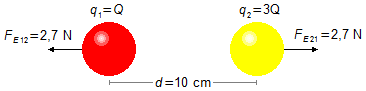
Solution

First, we need to convert the distance given in centimeters (cm) to meters (m) used in the International System of Units (SI).
\[ \begin{gather} d=10\;\mathrm{\cancel{cm}}\times\frac{1\;\mathrm m}{100\;\mathrm{\cancel{cm}}}=0,1\;\mathrm m=1\times10^{-1}\;\mathrm m \end{gather} \]
Applying Coulomb's Law, the magnitude of electric force is given by
\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;q_1\;||\;q_2\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;Q\;||\;3Q\;|}{d^2}\\[5pt] 3Q^2=\frac{F_{\small E}d^2}{k_e}\\[5pt] Q=\sqrt{\frac{F_{\small E}d^2}{3k_e}}\\[5pt] Q=\sqrt{\frac{\left(2,7\;\mathrm N\right)\left(1\times 10^{-1}\;\mathrm m\right)^2}{3\left(9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}}\right)}}\\[5pt] Q=\sqrt{\frac{\left(2,7\;\mathrm{\cancel N}\right)\left(1\times 10^{-2}\;\mathrm{\cancel{m^2}}\right)}{3\left(9\times 10^9\;\mathrm{\frac{\cancel N.\cancel{m^2}}{C^2}}\right)}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=1\times 10^{-6}\;\mathrm{C}} \end{gather} \]

Note: If the value of the small charge is q1 = 1 × 10−6 C, the value of the greatest is q2 = 3 × 1 × 10−6 = 3 × 10−6 C.
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .