Exercice Résolu sur les Force Électrique

Deux charges électriques positives et ponctuelles, dont l'une est le triple de l'autre, se repoussent avec une force de module 2,7 N dans le vide lorsque la distance entre elles est de 10 cm. Déterminer la plus petite des charges.
La Constante de Coulomb est   \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

 

Données du problème:

  • Charge 1:    q1 = Q;
  • Charge 2:    q2 = 3Q;
  • Force électrique de répulsion entre les charges:    FE = 2,7 N;
  • Distance entre les charges:    d = 10 cm;
  • Constante de Coulomb:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).

Schéma du problème:

La force FE12 est la force de répulsion sur la sphère 1 due à la sphère 2, la force FE21 est la force de répulsion sur la sphère 2 due à la sphère 1 ; en module, ces forces sont égales à FE (Figure 1).

Figure 1

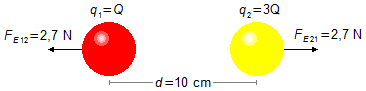
Solution:

Premièrement, nous devons convertir la distance donnée en centimètres (cm) en mètres (m) en utilisant le Système International d'Unité (SI).

\[ \begin{gather} d=10\;\mathrm{\cancel{cm}}\times\frac{1\;\mathrm m}{100\;\mathrm{\cancel{cm}}}=0,01\;\mathrm m=1\times10^{-2}\;\mathrm m \end{gather} \]

En appliquant la Loi de Coulomb, le module de la force électrique est donné par

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;q_1\;||\;q_2\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;Q\;||\;3Q\;|}{d^2} \\[5pt] 3Q^2=\frac{F_{\small E}d^2}{k_e} \\[5pt] Q=\sqrt{\frac{F_{\small E}d^2}{3k_e}} \\[5pt] Q=\sqrt{\frac{2,7\times 1\times 10^{-2}}{3\times 9\times 10^9}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {Q=1\times 10^{-6}\;\mathrm{C}} \end{gather} \]
Remarque: Si la charge la plus petite est q1 = 1×10−6 C, alors la charge la plus grande est q2 = 3×1×10−6 = 3×10−6 C.
Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .