Una carica puntiforme di 200 μC viene spostata da un punto A a un punto B all'interno di un campo elettrico. Il lavoro compiuto dalla forza elettrica è di 8×10⁻⁴ J. Calcolare:
a) La differenza di potenziale tra i punti A e B; b) Il potenziale elettrico di A prendendo B come riferimento.

Dati del problema:

• Carica elettrica:    q = 200 μC = 200×10⁻⁶ C;
• Lavoro compiuto dalla forza elettrica:    \( {_{{\small F}_{\small E}}}W{_a^b}=8\times 10^{-4}\;\mathrm J \) .

Schema del problema:

Figura 1

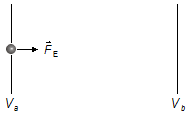
Soluzione:

a) Il lavoro della forza elettrica in funzione della carica e della differenza di potenziale è dato da

b) Assumiamo il potenziale del punto B come riferimento. Il potenziale di questo punto sarà nullo, V_b = 0. Sostituendo questo valore nell’equazione trovata nel punto precedente, il potenziale di A sarà