Eine Punktladung von 200 μC wird von einem Punkt A zu einem Punkt B in einem elektrischen Feld bewegt. Die durch die elektrische Kraft verrichtete Arbeit beträgt 8×10⁻⁴ J. Berechne:
a) Die Potentialdifferenz zwischen den Punkten A und B;
b) Das elektrische Potenzial von A, wobei B als Referenzpunkt genommen wird.

Gegebene Daten:

• Elektrische Ladung:    q = 200 μC = 200×10⁻⁶ C;
• Von der elektrischen Kraft verrichtete Arbeit:    \( {_{{\small F}_{\small E}}}W{_a^b}=8\times 10^{-4}\;\mathrm J \) .

Problem-Skizze:

Abb. 1

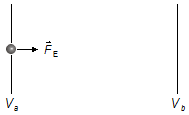
Lösung:

a) Die Arbeit der elektrischen Kraft als Funktion von der Ladung und der Potentialdifferenz ist gegeben durch

b) Wir nehmen das Potential des Punktes B als Referenz. Das Potential dieses Punktes ist null, also V_b = 0. Setzt man diesen Wert in die zuvor gefundene Gleichung ein, ergibt sich für das Potenzial von A