Esercizio Risolto di Forza Elettrica

L’atomo di idrogeno è costituito da un protone e un elettrone. Secondo il modello atomico di Bohr, l’elettrone descrive una traiettoria circolare con il protone al centro.
Dati:
massa dell’elettrone:    \( 9,1\times 10^{-31}\;\mathrm{kg} \) ;
velocità scalare dell’elettrone:    \( 2,2\times 10^6\;\mathrm{m/s} \) ;
carica del protone:    \( 1,6\times 10^{-19}\;\mathrm C \) ;
carica dell’elettrone:    \( -1,6\times 10^{-19}\;\mathrm C \) .
Determinare il raggio dell’orbita dell’elettrone per l’atomo nel vuoto.

Dati del problema:

Massa dell’elettrone: \( m=9,1\times 10^{-31}\;\mathrm{kg} \) ;
Velocità scalare dell’elettrone: \( v=2,2\times 10^6\;\mathrm{m/s} \) ;
Carica del protone: \( q_p=1,6\times 10^{-19}\;\mathrm C \) ;
Carica dell’elettrone: \( q_e=-1,6\times 10^{-19}\;\mathrm C \) ;
Costante di Coulomb nel vuoto: \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) .

Schema del problema:

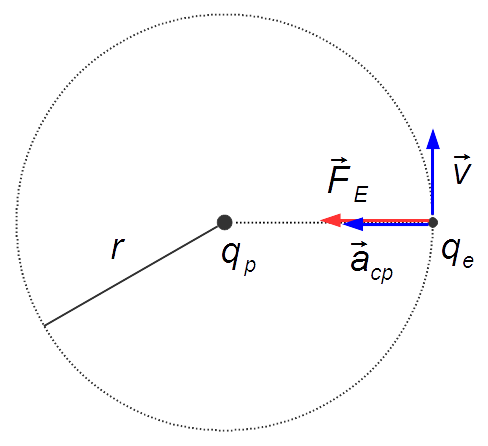
Sull’elettrone, di carica q_e, agiscono la velocità tangenziale \( \vec v \), la forza elettrica \( {\vec F}_{\small E} \) e la forza centripeta \( {\vec F}_{cp} \) (Figura 1).

Figura 1

Soluzione:

Applicando la Legge di Coulomb, il modulo della forza elettrica è dato da

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;Q\;||\;q\;|}{r^2}} \end{gather} \]

\[ \begin{gather} F_{\small E}=k_e\frac{|\;q_p\;||\;q_e\;|}{r^2} \tag{I} \end{gather} \]

L’elettrone compie un Moto Circolare Uniforme ed è soggetto all’azione della forza centripeta; scrivendo la Seconda Legge di Newton per un corpo in moto circolare

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{cp}=ma_{cp}} \tag{II} \end{gather} \]

l’accelerazione centripeta è data da

\[ \begin{gather} \bbox[#99CCFF,10px] {a_{cp}=\frac{v^2}{r}} \tag{III} \end{gather} \]

sostituendo l’equazione (III) nell’equazione (I)

\[ \begin{gather} F_{cp}=m\frac{v^2}{r} \tag{IV} \end{gather} \]

Il protone e l’elettrone possiedono cariche di segno opposto. La forza elettrica tra loro è attrattiva. Poiché questa forza coincide con la forza centripeta risultante, uguagliamo le equazioni (I) e (IV)

\[ \begin{gather} k_e\frac{|\;q_p\;||\;q_e\;|}{r^{\cancel 2}}=m\frac{v^2}{\cancel r} \\[5pt] r=k_e\frac{|\;q_p\;||\;q_e\;|}{m v^2} \\[5pt] r=9\times 10^9\times\frac{|\;1,6\times 10^{-19}\;|\times|\;-1,6\times 10^{-19}\;|}{9,1\times 10^{-31}\times\left(2,2\times 10^6\right)^2} \\[5pt] r=\frac{23,4\times 10^9\times 10^{-38}\times 10^{18}}{4,4} \\[5pt] \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {r\approx 5,3\times 10^{-11}\;\mathrm m} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .