Solved Problem on Coulomb's Law

The hydrogen atom is made up of one proton and one electron. According to Bohr's atomic model, the electron follows a circular trajectory with the proton in the center.
Data:
electron mass:   \( 9.1\times 10^{-31}\;\mathrm{kg} \) ;
electron speed:   \( 2.2\times 10^\;\mathrm C \) ;
proton charge:   \( 1.6\times 10^{-19}\;\mathrm C \) ;
electron charge:   \( -1.6\times 10^{-19}\;\mathrm C \) .
Determine the radius of the orbit of an electron for the atom in a vacuum.

Problem data:

Electron mass: \( m=9.1\times 10^{-31}\;\mathrm{kg} \) ;
Velocity of the electron: \( v=2.2\times 10^{6}\;\mathrm C \) ;
Charge of the proton: \( q_p=1.6\times 10^{-19}\;\mathrm C \) ;
Charge of the electron: \( q_e=-1.6\times 10^{-19}\;\mathrm C \) ;
Coulomb Constant in a vacuum: \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) .

Problem diagram:

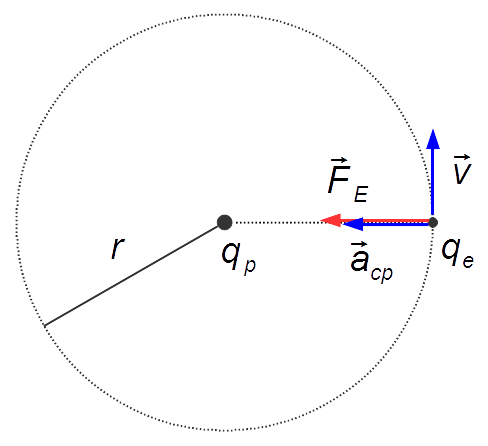
The tangential velocity \( \vec v \), the electric force \( {\vec F}_{\small E} \), and the centripetal force \( {\vec F}_{cp} \) acts on the electron, q_e (Figure 1).

Figure 1

Solution

Applying the Coulomb's law, the electric force is given, in magnitude, by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;Q\;||\;q\;|}{r^2}} \end{gather} \]

\[ \begin{gather} F_{\small E}=k_e\frac{|\;q_p\;||\;q_e\;|}{r^2} \tag{I} \end{gather} \]

The electron is in Uniform Circular Motion with constant speed, and a centripetal force acts on it, writing Newton's Second Law for a body in a circular motion

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{cp}=ma_{cp}} \tag{II} \end{gather} \]

the centripetal acceleration is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {a_{cp}=\frac{v^2}{r}} \tag{III} \end{gather} \]

substituting expression (III) into expression (I)

\[ \begin{gather} F_{cp}=m\frac{v^{2}}{r} \tag{IV} \end{gather} \]

The proton and the electron have charges with opposite signs. The electric force between them is attractive, as this force coincides with the resultant centripetal force, equating expressions (I) and (IV)

\[ \begin{gather} k_e\frac{|\;q_p\;||\;q_e\;|}{r^{\cancel 2}}=m\frac{v^2}{\cancel r}\\[5pt] r=k_e\frac{|\;q_p\;||\;q_e\;|}{m v^2}\\[5pt] r=\left(9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}}\right)\times \frac{|\;1.6\times 10^{-19}\;\mathrm C\;|\times|\;-1.6\times 10^{-19}\;\mathrm C\;|}{\left(9.1\times 10^{-31}\;\mathrm k\right)\times\left(2.2\times 10^{6}\;\mathrm{m/s}\right)^2}\\[5pt] r=\left(9\times 10^9\;\mathrm{\frac{N.\cancel{m^2}}{\cancel{C^2}}}\right)\left(\frac{2.6\times 10^{-38}\;\mathrm{\cancel{C^2}}}{4.4\times 10^{-18}\;\mathrm{\frac{kg.\cancel{m^2}}{s^2}}}\right)\\[5pt] r=\frac{23.4\times 10^9\times 10^{-38}\times 10^{18}\;\mathrm{\frac{\cancel{kg}.m}{\cancel{s^2}}}}{4.4\;\mathrm{\frac{\cancel{kg}}{\cancel{s^2}}}}\\[5pt] \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {r\approx 5.3\times 10^{-11}\;\mathrm m} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .