Exercice Résolu sur les Force Électrique
publicité   



L'atome d'hydrogène est constitué d'un proton et d'un électron. Selon le modèle atomique de Bohr, l'électron décrit une trajectoire circulaire avec le proton au centre.
Données:
masse de l'électron:   \( 9,1\times 10^{-31}\;\mathrm{kg} \) ;
vitesse scalaire de l'électron:   \( 2,2\times 10^\;\mathrm C \) ;
charge du proton:   \( 1,6\times 10^{-19}\;\mathrm C \) ;
charge de l'électron:   \( -1,6\times 10^{-19}\;\mathrm C \) .
Déterminer le rayon de l'orbite de l'électron pour l'atome dans le vide.


Données du problème:
  • Masse de l'électron:    \( m=9,1\times 10^{-31}\;\mathrm{kg} \) ;
  • Vitesse scalaire de l'électron:    \( v=2,2\times 10^{6}\;\mathrm C \) ;
  • Charge du proton:    \( q_p=1,6\times 10^{-19}\;\mathrm C \) ;
  • Charge de l'électron:    \( q_e=-1,6\times 10^{-19}\;\mathrm C \) ;
  • Constante de Coulomb dans le vide:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) .
Schéma du problème:

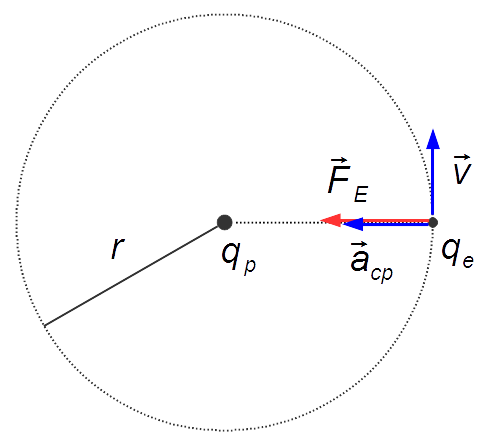
Pour l'électron, qe, agissent la vitesse tangentielle \( \vec v \), la force électrique \( {\vec F}_{\small E} \) et la force centripète \( {\vec F}_{cp} \) (Figure 1).
Figure 1

Solution

En appliquant la Loi de Coulomb, la force électrique est donnée, en module, par
\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;Q\;||\;q\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;q_p\;||\;q_e\;|}{r^2} \tag{I} \end{gather} \]
L'électron effectue un Mouvement Circulaire Uniforme, il est soumis à l'action de la force centripète, en écrivant la Deuxième Loi de Newton pour un corps en mouvement circulaire
\[ \begin{gather} \bbox[#99CCFF,10px] {F_{cp}=ma_{cp}} \tag{II} \end{gather} \]
l'accélération centripète est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {a_{cp}=\frac{v^2}{r}} \tag{III} \end{gather} \]
en remplaçant l'équation (III) dans l'équation (I)
\[ \begin{gather} F_{cp}=m\frac{v^2}{r} \tag{IV} \end{gather} \]
Le proton et l'électron ont des charges de signes opposés. La force électrique entre eux est attractive, comme cette force coïncide avec la force centripète résultante, en égalant les équations (I) et (IV).
\[ \begin{gather} k_e\frac{|\;q_p\;||\;q_e\;|}{r^{\cancel 2}}=m\frac{v^2}{\cancel r}\\[5pt] r=k_e\frac{|\;q_p\;||\;q_e\;|}{m v^2}\\[5pt] r=9\times 10^9\times\frac{|\;1,6\times 10^{-19}\;|\times|\;-1,6\times 10^{-19}\;|}{9,1\times 10^{-31}\times\left(2,2\times 10^{6}\right)^2}\\[5pt] r=\frac{23,4\times 10^9\times 10^{-38}\times 10^{18}}{4,4}\\[5pt] \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {r\approx 5,3\times 10^{-11}\;\mathrm m} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .