Ejercicio Resuelto sobre Fuerza Eléctrica
publicidad   



El átomo de hidrógeno está constituido por un protón y un electrón. Según el modelo atómico de Bohr, el electrón describe una trayectoria circular con el protón en el centro.
Datos:
masa del electrón:   \( 9,1\times 10^{-31}\;\mathrm{kg} \) ;
velocidad escalar del electrón:   \( 2,2\times 10^\;\mathrm C \) ;
carga del protón:   \( 1,6\times 10^{-19}\;\mathrm C \) ;
carga del electrón:   \( -1,6\times 10^{-19}\;\mathrm C \) .
Determinar el radio de la órbita del electrón para el átomo en el vacío.


Datos del problema:
  • Masa del electrónn:    \( m=9,1\times 10^{-31}\;\mathrm{kg} \) ;
  • Velocidad escalar del electrón:    \( v=2,2\times 10^{6}\;\mathrm C \) ;
  • Carga del protón:    \( q_p=1,6\times 10^{-19}\;\mathrm C \) ;
  • Carga del electrón:    \( q_e=-1,6\times 10^{-19}\;\mathrm C \) ;
  • Constante de Coulomb en el vacío:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) .
Esquema del problema:

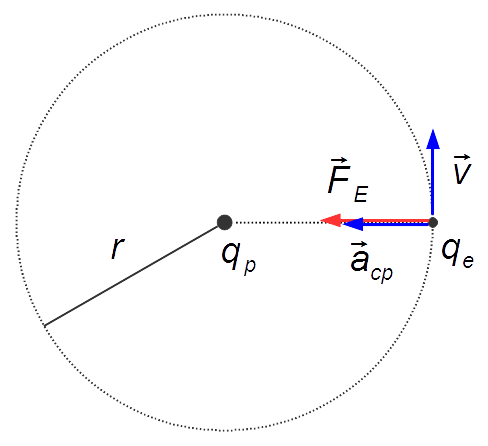
En el electrón, qe, actúan la velocidad tangencial \( \vec v \), la fuerza eléctrica \( {\vec F}_{\small E} \) y la fuerza centrípeta \( {\vec F}_{cp} \) (Figura 1).
Figura 1

Solución

Aplicando la Ley de Coulomb, la fuerza eléctrica se expresa, en módulo, como
\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;Q\;||\;q\;|}{r^2}} \end{gather} \]
\[ \begin{gather} F_{\small E}=k_e\frac{|\;q_p\;||\;q_e\;|}{r^2} \tag{I} \end{gather} \]
El electrón realiza un Movimiento Circular Uniforme (MCU), está bajo la acción de la fuerza centrípeta, escribiendo la Segunda Ley de Newton para un cuerpo en movimiento circular
\[ \begin{gather} \bbox[#99CCFF,10px] {F_{cp}=ma_{cp}} \tag{II} \end{gather} \]
la aceleración centrípeta está dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {a_{cp}=\frac{v^2}{r}} \tag{III} \end{gather} \]
sustituyendo la ecuación (III) en la ecuación (I)
\[ \begin{gather} F_{cp}=m\frac{v^2}{r} \tag{IV} \end{gather} \]
El protón y el electrón poseen cargas con signos opuestos. La fuerza eléctrica entre ellos es de atracción, ya que esta fuerza coincide con la fuerza centrípeta resultante, igualando las ecuaciones (I) y (IV).
\[ \begin{gather} k_e\frac{|\;q_p\;||\;q_e\;|}{r^{\cancel 2}}=m\frac{v^2}{\cancel r}\\[5pt] r=k_e\frac{|\;q_p\;||\;q_e\;|}{m v^2}\\[5pt] r=9\times 10^9\times\frac{|\;1,6\times 10^{-19}\;|\times|\;-1,6\times 10^{-19}\;|}{9,1\times 10^{-31}\times\left(2,2\times 10^{6}\right)^2}\\[5pt] r=\frac{23,4\times 10^9\times 10^{-38}\times 10^{18}}{4,4}\\[5pt] \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {r\approx 5,3\times 10^{-11}\;\mathrm m} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .