Gelöste Übung zur Elektrischen Kraft

Das Wasserstoffatom besteht aus einem Proton und einem Elektron. Nach dem atomaren Bohr-Modell beschreibt das Elektron eine Kreisbahn mit dem Proton im Mittelpunkt.
Gegeben:
Masse des Elektrons:    \( 9,1\times 10^{-31}\;\mathrm{kg} \) ;
Betrag der Geschwindigkeit des Elektrons:    \( 2,2\times 10^6\;\mathrm{m/s} \) ;
Ladung des Protons:    \( 1,6\times 10^{-19}\;\mathrm C \) ;
Ladung des Elektrons:    \( -1,6\times 10^{-19}\;\mathrm C \) .
Gesucht ist der Radius der Elektronenbahn im Vakuum.

Gegebene Daten:

Masse des Elektrons: \( m=9,1\times 10^{-31}\;\mathrm{kg} \) ;
Betrag der Geschwindigkeit des Elektrons: \( v=2,2\times 10^6\;\mathrm{m/s} \) ;
Ladung des Protons: \( q_p=1,6\times 10^{-19}\;\mathrm C \) ;
Ladung des Elektrons: \( q_e=-1,6\times 10^{-19}\;\mathrm C \) ;
Coulomb-Konstante im Vakuum: \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) .

Schema des Problems:

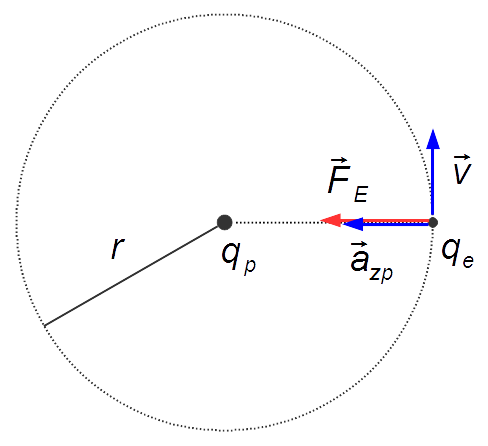
Auf das Elektron mit der Ladung q_e wirken die Tangentialgeschwindigkeit \( \vec v \), die elektrische Kraft \( {\vec F}_{\small E} \) und die Zentripetalkraft \( {\vec F}_{zp} \) (Abbildung 1).

Abb. 1

Lösung:

Anwendung des Coulomb-Gesetzes wird der Betrag der elektrischen Kraft gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{\small E}=k_e\frac{|\;Q\;||\;q\;|}{r^2}} \end{gather} \]

\[ \begin{gather} F_{\small E}=k_e\frac{|\;q_p\;||\;q_e\;|}{r^2} \tag{I} \end{gather} \]

Das Elektron führt eine Gleichförmige Kreisbewegung aus und steht unter dem Einfluss der Zentripetalkraft. Formuliert man das 2. Newtonsche Gesetz für einen Körper in Kreisbewegung, erhält man

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{zp}=ma_{zp}} \tag{II} \end{gather} \]

Die Zentripetalbeschleunigung ist gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {a_{zp}=\frac{v^2}{r}} \tag{III} \end{gather} \]

Setzt man Gleichung (III) in Gleichung (I) ein, ergibt sich

\[ \begin{gather} F_{zp}=m\frac{v^2}{r} \tag{IV} \end{gather} \]

Das Proton und das Elektron besitzen entgegengesetzte Ladungen. Die zwischen ihnen wirkende elektrische Kraft ist daher eine Anziehungskraft. Da diese Kraft gleichzeitig die resultierende Zentripetalkraft ist, setzt man Gleichung (I) und Gleichung (IV) gleich

\[ \begin{gather} k_e\frac{|\;q_p\;||\;q_e\;|}{r^{\cancel 2}}=m\frac{v^2}{\cancel r} \\[5pt] r=k_e\frac{|\;q_p\;||\;q_e\;|}{m v^2} \\[5pt] r=9\times 10^9\times\frac{|\;1,6\times 10^{-19}\;|\times|\;-1,6\times 10^{-19}\;|}{9,1\times 10^{-31}\times\left(2,2\times 10^6\right)^2} \\[5pt] r=\frac{23,4\times 10^9\times 10^{-38}\times 10^{18}}{4,4} \\[5pt] \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {r\approx 5,3\times 10^{-11}\;\mathrm m} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .