Kinematics
advertisement
A particle describes a curve in a plane, such as its positions relative to an orthogonal Cartesian system,
taken in that plan, vary with time according to equations:
\[
\begin{gather}
x=t^{3}-2t\\[8pt]
y=4t^{2}
\end{gather}
\]
where x and y are in meters and t in seconds. Determine the speed and acceleration of
the point at instant t = 2 s.
A body describes on a plane a curve given by the equations:
\[
\begin{gather}
x=3\cos t-\cos 2t\\
y=3\sin t-\sin 2t
\end{gather}
\]
where x and y are given in meters and t in seconds. Determine the speed and
acceleration of the body at instant t = π/2 s.
Determine the acceleration vector of a body that slides from the rest by a helicoid channel with pitch
k and radius R at the end of the n-th turns, the friction is neglected.

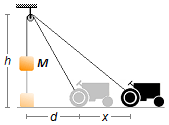
A load with mass M is on the ground, a tractor raises the load moving with constant speed
v. The initial distance of the tractor to the load is equal to d and the pulley is at a
height of h. The pulley is lightweight and frictionless, and the hope is inextensible, calculate
the ascent speed of the load.
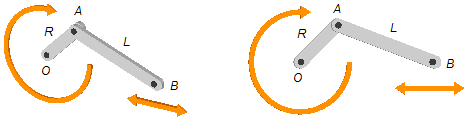
In the hand-crank/rod system shown in the figure, the OA crank has constant angular speed ω
and length R, the rod has a length L.
a) Determine the parametric equations of the trajectory of any point of the rod;
b) Under what conditions the trajectory described by this point is elliptical?
c) Determine the equations of point A of the end of the crank;
d) Determine the equations of point B of the rod end.
a) Determine the parametric equations of the trajectory of any point of the rod;
b) Under what conditions the trajectory described by this point is elliptical?
c) Determine the equations of point A of the end of the crank;
d) Determine the equations of point B of the rod end.
Particle B starts a motion from point O at the same time particle A passes through
this point. Both particles run the same straight path and the curves in the velocity-time graph are a
quarter of circumference with equal radius, as shown in the figure. Determine:
a) The time in which particles have the same speed;
b) The value of this speed;
c) The time in particles have the same acceleration in magnitude;
d) The value of this acceleration.
a) The time in which particles have the same speed;
b) The value of this speed;
c) The time in particles have the same acceleration in magnitude;
d) The value of this acceleration.

Find the expressions for the velocity and acceleration of a body, which moves in a plane, in polar
coordinates.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .