Solved Problem in Kinematics

Solved Problem on Kinematics

In the hand-crank/rod system shown in the figure, the OA crank has constant angular speed ω and length R, the rod has a length L.
a) Determine the parametric equations of the trajectory of any point of the rod;
b) Under what conditions the trajectory described by this point is elliptical?
c) Determine the equations of point A of the end of the crank;
d) Determine the equations of point B of the rod end.

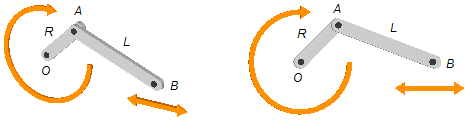
Problem data:

Angular speed of crank: ω;
Length of the crank: R;
Length of rod: L.

Problem diagram:

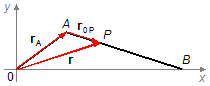
We choose a reference frame at point O and a point P on the rod AB. The position vector r_A describes the motion of point A at the crank, the vector r_OP describes the motion of point P relative to point A (relative motion) and the vector r describes the motion of point P relative to the reference frame in O. The point A rotates around it describing a circumference with radius R (length of the crank) while the point B in the rod describes a motion along the x-axis (Figure 1).

Figure 1

Solution

a) The position vector of point P is given by

\[ \bbox[#99CCFF,10px] {\mathbf{r}=\mathbf{r}_{A}+\mathbf{r}_{OP}} \]

With Figure 2, we can write

\[ \begin{gather} \mathbf{r}_{A}=R\cos \theta\;\mathbf{i}+R\operatorname{sen}\theta\;\mathbf{j}\\ {{\mathbf{r}}}_{OP}=d\cos\phi \;\mathbf{i}-d\operatorname{sen}\phi\;\mathbf{j} \end{gather} \]

where d is the distance from point A to point P, and i and j are the unit vectors in x and y directions. The vector position can be written as

\[ \mathbf{r}=R\cos \theta\;\mathbf{i}+R\operatorname{sen}\theta\;\mathbf{j}+d\cos \phi\;\mathbf{i}-d\operatorname{sen}\phi \;\mathbf{j} \tag{I} \]

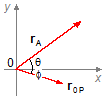
Figure 2

The segment \( \overline{{AB}} \) (rod) makes an angle ϕ with the x-axis, the same angle between the vector r_OP and the horizontal line (Figure 3-A). Drawing an auxiliary line by point A to the x-axis, in point M we have the height h, which determines the triangles ΔMOA and ΔMBA (Figure 3-B). From the triangle ΔMOA, we find the height h

\[ \begin{gather} \operatorname{sen}\theta =\frac{h}{R}\\ h=R\operatorname{sen}\theta \tag{II} \end{gather} \]

Figure 3

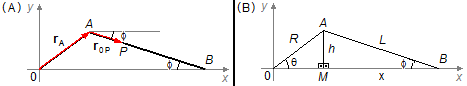
Using the Pythagorean Theorem, we determine the side x of the triangle ΔMBA

\[ \begin{gather} L^{2}=h^{2}+x^{2}\\ x^{2}=L^{2}-h^{2} \tag{III} \end{gather} \]

substituting the expression (II) into expression (III)

\[ \begin{gather} x^{2}=L^{2}-R^{2}\operatorname{sen}^{2}\theta\\ x=\left(L^{2}-R^{2}\operatorname{sen}^{2}\theta\right)^{\frac{1}{2}} \tag{IV} \end{gather} \]

Writing the cos ϕ as a function of the variable θ

\[ \begin{gather} \cos \phi =\frac{x}{L} \tag{V} \end{gather} \]

substituting the expression (IV) into expression (V)

\[ \begin{gather} \cos \phi =\frac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\theta\right)^{\frac{1}{2}}}{L} \tag{VI} \end{gather} \]

Writing the sen ϕ as a function of the variable θ

\[ \begin{gather} \operatorname{sen}\phi =\frac{h}{L} \tag{VII} \end{gather} \]

substituting the expression (II) into expression (VII)

\[ \begin{gather} \operatorname{sen}\phi =\frac{R\operatorname{sen}\theta }{L} \tag{VIII} \end{gather} \]

substituting expressions (VI) and (VIII) into expression (I)

\[ \mathbf{r}=R\cos \theta\;\mathbf{i}+R\operatorname{sen}\theta\;\mathbf{j}+d\frac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\theta\right)^{\frac{1}{2}}}{L}\;\mathbf{i}-d\frac{R\operatorname{sen}\theta}{L}\;\mathbf{j} \]

we have \( \theta =\omega t \) and \( \mathbf{r}=x\;\mathbf{i}+y\;\mathbf{j} \), the parametric equations are

\[ \begin{gather} x\;\mathbf{i}+y\;\mathbf{j}=R\cos \omega t\;\mathbf{i}+R\operatorname{sen}\omega t\;\mathbf{j}+d\frac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{L}\;\mathbf{i}-d\frac{R\operatorname{sen}\omega t}{L}\;\mathbf{j}\\ x\;\mathbf{i}+y\;\mathbf{j}=\left[R\cos\omega t+d\frac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{L}\right]\;\mathbf{i}+R\operatorname{sen}\omega t\left[1-d\frac{1}{L}\right]\;\mathbf{j}\\ x\;\mathbf{i}+y\;\mathbf{j}=\left[R\cos\omega t+d\frac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{L}\right]\;\mathbf{i}+\frac{R}{L}\operatorname{sen}\omega t\left[L-d\right]\;\mathbf{j} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {\begin{array}{l} x=R\cos \omega t+d\dfrac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{L}\\[5pt] y=\dfrac{R}{L}\operatorname{sen}\omega t\left(L-d\right) \end{array}} \]

b) If the length of the crank is equal to the length of the rod, R = L, substituting this condition in the result of the previous item

\[ \begin{array}{l} x=R\cos \omega t+d\dfrac{\left(R^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{R}\\ y=\dfrac{R}{R}\operatorname{sen}\omega t\left(R-d\right)\\[10pt] x=R\cos \omega t+d\dfrac{\left[R^{2}\left(1-\operatorname{sen}^{\;2}\omega t\right)\right]^{\frac{1}{2}}}{R}\\ y=\operatorname{sen}\omega t\left(R-d\right)\\[10pt] x=R\cos \omega t+dR\dfrac{\left(1-\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{R}\\ y=\operatorname{sen}\omega t\left(R-d\right)\\[10pt] x=R\cos \omega t+d\left(1-\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}\\ y=\operatorname{sen}\omega t\left(R-d\right) \end{array} \]

we have \( \left(1-\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}=\cos \omega t \)

\[ \begin{array}{l} x=R\cos \omega t+d\cos \omega t\\ y=\operatorname{sen}\omega t\left(R-d\right)\\[10pt] x=\cos \omega t\left(R+d\right)\\ y=\operatorname{sen}\omega t\left(R-d\right) \end{array} \]

squaring both sides of the equations, and adding the two equations

\[ \begin{gather} x^{2}=\left[\cos \omega t\left(R+d\right)\right]^{2}\\ y^{2}=\left[\operatorname{sen}\omega t\left(R-d\right)\right]^{2}\\[10pt] x^{2}=\cos ^{2}\omega t\left(R+d\right)^{2}\\ y^{2}=\operatorname{sen}^{2}\omega t\left(R-d\right)^{2}\\[10pt] \frac{x^{2}}{\left(R+d\right)^{2}}=\cos ^{2}\omega t\\ \frac{(\text{+})\qquad \dfrac{y^{2}}{\left(R-d\right)^{2}}=\operatorname{sen}^{2}\omega t \qquad\qquad }{\dfrac{x^{2}}{\left(R+d\right)^{2}}+\dfrac{y^{2}}{\left(R-d\right)^{2}}=\cos^{2}\omega t+\operatorname{sen}^{2}\omega t} \end{gather} \]

we have \( \cos \omega t+\operatorname{sen}^{2}\omega t=1 \)

\[ \bbox[#FFCCCC,10px] {\frac{x^{2}}{\left(R+d\right)^{2}}+\frac{y^{2}}{\left(R-d\right)^{2}}=1} \]

this is an ellipse with a major axis equal to (R+d) and a minor axis (R−d).

c) For point A the distance d is zero (d = 0, point P coincides with point A), substituting this condition in item (a)

\[ \begin{array}{l} x=R\cos \omega t+0.\dfrac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{L}\\ y=\dfrac{R}{L}\operatorname{sen}\omega t\left(L-0\right)\\[10pt] x=R\cos \omega t+0\\ y=\dfrac{R}{L}\operatorname{sen}\omega tL \end{array} \]

\[ \bbox[#FFCCCC,10px] {\begin{array}{l} x=R\cos \omega t\\[5pt] y=R\operatorname{sen}\omega t \end{array}} \]

these equations represent a point describing a circumference with radius R (as expected).

d) For point B at distance d is equal to L (d = L, point P coincides with point B), substituting this condition in item (a)

\[ \begin{array}{l} x=R\cos \omega t+L .\dfrac{\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}}{L}\\ y=\dfrac{R}{L}\operatorname{sen}\omega t\left(L-L\right)\\[10pt] x=R\cos \omega t+\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}\\ y=\dfrac{R}{L}\operatorname{sen}\omega t .0 \end{array} \]

\[ \bbox[#FFCCCC,10px] {\begin{array}{l} x=R\cos \omega t+\left(L^{2}-R^{2}\operatorname{sen}^{2}\omega t\right)^{\frac{1}{2}}\\[5pt] y=0 \end{array}} \]

These equations represent a point moving only on the x-axis.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .