Solved Problem on Kinematics
advertisement
Find the expressions for the velocity and acceleration of a body, which moves in a plane, in polar coordinates.
Solution
The position vector in polar coordinates is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{r}=r\;\mathbf{e}_{r}} \tag{I}
\end{gather}
\]
The velocity v is the derivative of position with respect to time. In polar coordinates, the unit
vectors er and eθ change position with time. They are
functions of time.
From the Integral and Differential Calculus, the product rule for differentiation is given by
\[
\frac{d(fg)}{dt}=\frac{df}{dt}g+f\frac{dg}{dt}
\]
\[
\begin{gather}
\frac{d\mathbf{r}}{dt}=\frac{dr}{dt}\;\mathbf{e}_{r}+r\frac{d\mathbf{e}_{r}}{dt} \tag{II}
\end{gather}
\]
The unit vector er is a function of angle θ, to find
\( \frac{d\mathbf{e}_{r}}{dt} \)
we apply the chain rule.
From the Integral and Differential Calculus, the chain rule is given by
\[
\frac{df[g(t)]}{dt}=\frac{df}{dg}\frac{dg}{dt}
\]
\[
\begin{gather}
\frac{d\mathbf{e}_{r}}{dt}=\frac{d\mathbf{e}_{r}}{d\theta}\frac{d\theta}{dt} \tag{III}
\end{gather}
\]
When position r moves to the position r+dr, we have an infinitesimal change of the
angle dθ (Figure 1).
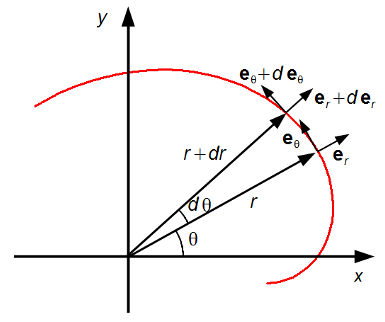
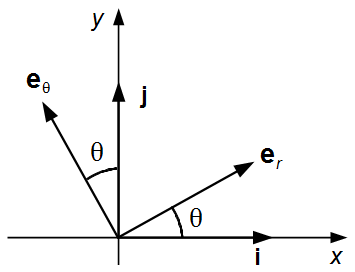
Plotting the unit vectors, er and eθ of the polar
coordinates, in a xy plane, we can find its components using unit vectors i and j
of the cartesian coordinates system (Figure 2).
\[
\begin{gather}
{\mathbf{e}}_{r}=\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j} \tag{IV-a}\\
{\mathbf{e}}_{\theta}=-\operatorname{sen}\theta \;\mathbf{i}+\cos \theta\;\mathbf{j} \tag{IV-b}
\end{gather}
\]
Differentiating the expression (IV-a) with respect to θ
\[
\frac{d{\mathbf{e}}_{r}}{d\theta}=\underbrace{-\operatorname{sen}\theta\;\mathbf{i}+\cos \theta\;\mathbf{j}}_{{\mathbf{e}}_{\theta}}
\]
\[
\begin{gather}
\frac{d\mathbf{e}_{r}}{d\theta}=\mathbf{e}_{\theta} \tag{V}
\end{gather}
\]
substituting the expression (V) into expression (III)
\[
\begin{gather}
\frac{d\mathbf{e}_{r}}{dt}=\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta} \tag{VI}
\end{gather}
\]
substituting the expression (VI) into expression (II), we have the speed
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{d\mathbf{r}}{dt}=\frac{dr}{dt}\;{\mathbf{e}}_{r}+r\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}} \tag{VII-a}
\end{gather}
\]
or using the following notation
\( \frac{d\mathbf{r}}{dt}=\dot{\mathbf{r}} \),
\( \frac{dr}{dt}=\dot{r} \)
and
\( \frac{d\theta}{dt}=\dot{\theta} \)
we can also write
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\dot{\mathbf{r}}=\dot{r}\;{\mathbf{e}}_{r}+r\dot{\theta}\;{\mathbf{e}}_{\theta}} \tag{VII-b}
\end{gather}
\]
or using the following notation
\( \dot{\mathbf{r}}=\mathbf{v} \),
\( \dot{r}=v_{r} \)
and
\( \dot{\theta}=\omega \)
can also write
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{v}=v_{r}\;{\mathbf{e}}_{r}+r\omega\;{\mathbf{e}}_{\theta}} \tag{VII-c}
\end{gather}
\]
To find the acceleration vector, we find the derivative with respect to time. We will use the velocity in
the form of the expression (VII-a).
From the Integral and Differential Calculus, the derivative of the sum is the sum of the derivatives
\[
\frac{d(f+g)}{dt}=\frac{df}{dt}+\frac{dg}{dt}
\]
\[
\begin{gather}
\frac{d}{dt}\frac{d\mathbf{r}}{dt}=\frac{d}{dt}\left(\frac{dr}{dt}\;{\mathbf{e}}_{r}\right)+\frac{d}{dt}\left(r\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}\right) \tag{VIII}
\end{gather}
\]
The first term on the right-hand side of the equation is the product of two functions and the second term
is the product of three functions, using the product rule
\[
\begin{gather}
\frac{d^{2}\mathbf{r}}{dt^{2}}=\left(\frac{d^{2}r}{dt^{2}}\;{\mathbf{e}}_{r}+\frac{dr}{dt}\frac{d{\mathbf{e}}_{r}}{dt}\right)+\left(\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{e}}_{\theta}+r\frac{d\theta}{dt}\frac{d{\mathbf{e}}_{\theta}}{dt}\right) \tag{IX}
\end{gather}
\]
The term
\( \frac{d\mathbf{e}_{r}}{dt} \)
has been found in the expression (V).The unit vector eθ is a function of angle θ, to find \( \frac{d\mathbf{e}_{\theta}}{dt} \) we apply the chain rule.
\[
\begin{gather}
\frac{d\mathbf{e}_{\theta}}{dt}=\frac{d\mathbf{e}_{\theta}}{d\theta}\frac{d\theta}{dt} \tag{X}
\end{gather}
\]
Differentiating the expression (IV-b) with respect to θ,
\[
\begin{gather}
\frac{d{\mathbf{e}}_{\theta }}{d\theta}=-\cos \theta \;\mathbf{i}-\operatorname{sen}\theta\;\mathbf{j}\\
\frac{d{\mathbf{e}}_{\theta}}{d\theta }=-(\underbrace{\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j}}_{{\mathbf{e}}_{r}})
\end{gather}
\]
\[
\begin{gather}
\frac{d\mathbf{e}_{\theta}}{d\theta}=-\mathbf{e}_{r} \tag{XI}
\end{gather}
\]
substituting the expression (XI) into expression (X)
\[
\begin{gather}
\frac{d\mathbf{e}_{\theta}}{dt}=-{\frac{d\theta}{dt}}\mathbf{e}_{r} \tag{XII}
\end{gather}
\]
substituting expressions (VI) and (XII) into expression (IX)
\[
\begin{gather}
\frac{d^{2}\mathbf{r}}{dt^{2}}=\left[\frac{d^{2}r}{dt^{2}}\;{\mathbf{e}}_{r}+\frac{dr}{dt}\left(\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}\right)\right]+\left[\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{e}}_{\theta}-r\frac{d\theta}{dt}\left(\frac{d\theta}{dt}\mathbf{e}_{r}\right)\right]\\
\frac{d^{2}\mathbf{r}}{dt^{2}}=\frac{d^{2}r}{dt^{2}}\;{\mathbf{e}}_{r}+\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}+\frac{dr}{dt}\frac{d\theta}{dt}\;{\mathbf{e}}_{\theta}+r\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{e}}_{\theta}-r\left(\frac{d\theta}{dt}\right)^{2}\mathbf{e}_{r}
\end{gather}
\]
Note: Do not confuse
\( \frac{d}{dt}\left(\frac{d\theta}{dt}\right)=\frac{d^{2}\theta}{dt^{2}} \)
which represents the second derivative of theta with respect to time, with
\( \frac{d\theta}{dt}\left(\frac{d\theta}{dt}\right)=\left(\frac{d\theta}{dt}\right)^{2} \)
, which represents the derivative of theta with respect to time squared.
\[ \bbox[#FFCCCC,10px]
{\frac{d^{2}\mathbf{r}}{dt^{2}}=\left(\frac{d^{2}r}{dt^{2}}-r\left(\frac{d\theta}{dt}\right)^{2}\right)\mathbf{e}_{r}+\left(2\frac{dr}{dt}\frac{d\theta}{dt}+r\frac{d^{2}\theta}{dt^{2}}\right)\;{\mathbf{e}}_{\theta}}
\]
or using the following notation
\( \frac{d^{2}\mathbf{r}}{dt^{2}}=\ddot{\mathbf{r}} \),
\( \frac{dr}{dt}=\dot{r} \),
\( \frac{d^{2}r}{dt^{2}}=\ddot{r} \),
\( \frac{d\theta}{dt}=\dot{\theta} \)
and
\( \frac{d^{2}\theta}{dt^{2}}=\ddot{\theta} \)
we can also write
\[ \bbox[#FFCCCC,10px]
{\ddot{\mathbf{r}}=\left(\ddot{r}-r{\dot{\theta}}^{2}\right)\mathbf{e}_{r}+\left(2\dot{r}\dot{\theta}+r\ddot{\theta}\right)\;{\mathbf{e}}_{\theta}}
\]
or using the following notation
\( \ddot{\mathbf{r}}=\mathbf{a} \)
we can also write
\[ \bbox[#FFCCCC,10px]
{\mathbf{a}=\left(\ddot{r}-r{\dot{\theta}}^{2}\right)\mathbf{e}_{r}+\left(2\dot{r}\dot{\theta}+r\ddot{\theta}\right)\;{\mathbf{e}}_{\theta}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .