Solved Problem on Kinematics
advertisement
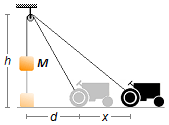
A load with mass M is on the ground, a tractor raises the load moving with constant speed
v. The initial distance of the tractor to the load is equal to d and the pulley is at a
height of h. The pulley is lightweight and frictionless, and the hope is inextensible, calculate
the ascent speed of the load.
Problem data:
- Mass of load: M;
- Tractor speed: v;
- Distance from the tractor to the load: d;
- Pulley height: h.
In Figure 1-A, we have the initial and final situations of the problem. Assuming the ground is horizontal and the rope that supports the load vertically The problem is reduced to two right triangles with 90° angle in \( \hat B \) (Figure 1-B).
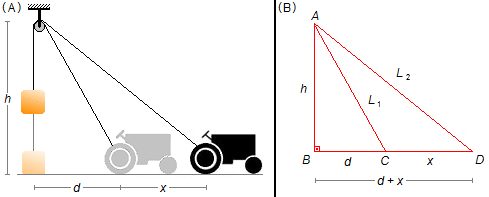
In the initial situation, we have the ΔABC triangle of sides h and d and hypotenuse L1 and in the final situation the ΔABD triangle of sides h and (d+x) and hypotenuse L2.
Solution
Calculating the hypotenuses of the two triangles by the Pythagorean Theorem
\[
\begin{gather}
L_{1}^{2}=d^{2}+h^{2}\\
L_{1}=\left(d^{2}+h^{2}\right)^{\frac{1}{2}}
\end{gather}
\]
\[
\begin{gather}
L_{2}^{2}=(d+x)^{2}+h^{2}\\
L_{2}=\left[(d+x)^{2}+h^{2}\right]^{\frac{1}{2}}
\end{gather}
\]
Calculating the difference between L2 and L1, we have the length of
rope y that tractor pulled when it moved from x (Figure 2).
\[
\begin{gather}
y=L_{2}-L_{1}\\
y=\left[(d+x)^{2}+h^{2}\right]^{\frac{1}{2}}-\left(d^{2}+h^{2}\right)^{\frac{1}{2}}
\end{gather}
\]
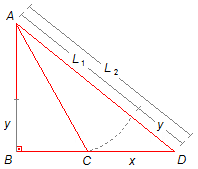
This expression gives the displacement of the load, as the speed is the derivative of displacement with respect to time, differentiating this expression we have the speed with which the load rises \( \left(v_{y}=\dfrac{dy}{dt}\right) \).
Differentiation of
\( y=\left[(d+x)^{2}+h^{2}\right]^{\frac{1}{2}}-\left(d^{2}+h^{2}\right)^{\frac{1}{2}} \)
The function y(x) is a composite function
The derivative is given by the chain rule
Substituting expressions (II), (III), and (IV) and the derivative of x with respect to time into expression (I)
\[ y=\left[(d+x)^{2}+h^{2}\right]^{\frac{1}{2}}-\left(d^{2}+h^{2}\right)^{\frac{1}{2}} \]
The function y(x) is a composite function
\[
y(u)=\left[u\right]^{\frac{1}{2}}-\left(d^{2}+h^{2}\right)^{\frac{1}{2}}
\]
\[
u(w)=(w)^{2}+h^{2}
\]
\[
w(x)=(d+x)
\]
and the variable x is a function of time x(t).The derivative is given by the chain rule
\[
\begin{gather}
\frac{dy[u(w(x(t)))]}{dt}=\frac{dy}{du}\frac{du}{dw}\frac{dw}{dx}\frac{dx}{dt} \tag{I}
\end{gather}
\]
the derivatives will be
\[
\begin{gather}
\frac{dy}{du}=\frac{1}{2}\left[u\right]^{\frac{1}{2}-1}-\underbrace{\left(d^{2}+h^{2}\right)^{\frac{1}{2}}}_{0}=\frac{1}{2}\left[u\right]^{\frac{-{1}}{2}}=\frac{1}{2u^{\frac{1}{2}}} \tag{II}
\end{gather}
\]
as d and h are constant the derivative of the second term is zero (constant derivative is
zero).
\[
\begin{gather}
\frac{du}{dw}=2w^{2-1}+\underbrace{h^{2}}_{0}=2w \tag{III}
\end{gather}
\]
as h is constant the derivative of the second term is zero.
\[
\begin{gather}
\frac{dw}{dx}=\underbrace{d}_{0}+1=1 \tag{IV}
\end{gather}
\]
as d is constant the derivative of the first term is zero.Substituting expressions (II), (III), and (IV) and the derivative of x with respect to time into expression (I)
\[
\begin{align}
\frac{dy}{dt}&=\frac{1}{2u^{\frac{1}{2}}}2w.1.\frac{dx}{dt}=\frac{w}{u^{\frac{1}{2}}}\frac{dx}{dt}=\\
&=\frac{(d+x)}{[(w)^{2}+h^{2}]^{\frac{1}{2}}}\frac{dx}{dt}=\frac{(d+x)}{[(d+x)^{2}+h^{2}]^{\frac{1}{2}}}\frac{dx}{dt}
\end{align}
\]
As \( v=\dfrac{dx}{dt} \) is the speed of the tractor given in the problem
\[ \bbox[#FFCCCC,10px]
{v_{y}=\frac{(d+x)v}{[(d+x)^{2}+h^{2}]^{\frac{1}{2}}}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .