In un punto di San Paolo (città brasiliana), il vettore del campo magnetico terrestre ha modulo \( B_{\small T}=8 \pi \times 10^{–6} \mathrm T \). In questo punto, si colloca un solenoide in modo che il suo asse sia parallelo al campo terrestre \( \vec B_{\small T} \). La lunghezza del solenoide è di 0,25 m e possiede 500 spire. Calcolare l’intensità della corrente affinché il campo magnetico al suo interno sia nullo. Permeabilità magnetica del vuoto   \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Dati del problema:

• Lunghezza del solenoide:    ℓ = 0,25 m;
• Numero di spire del solenoide:    N = 500 spire;
• Campo magnetico nel luogo:    \( B_{\small T}=8 \pi \times 10^{–6} \mathrm T \);
• Permeabilità Magnetica del vuoto:    \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Schema del problema:

Adottiamo la direzione del campo magnetico terrestre \( \vec B_{\small T} \), come positiva (Figura 1).

Figura 1

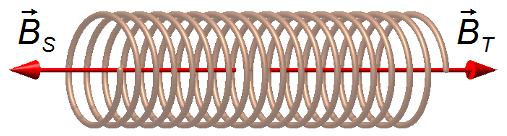
Soluzione:

Il vettore risultante del campo magnetico è dato da

In modulo, affinché la risultante del campo magnetico sia nulla, abbiamo la condizione

Il modulo del campo magnetico generato da un solenoide è dato da

sostituendo l’equazione (II) del campo magnetico del solenoide nell’equazione (I)