Exercice Résolu sur les Mouvement Unidimensionnel
EN
ES
PT-BR
publicité
Deux voitures participent à une course de dragsters sur une distance de 402 m (la distance la plus courante pour un quart de mile). Les voitures partent du repos. La voiture A a une accélération de 5 m/s2 et atteint une vitesse maximale de 36 m/s, tandis que la voiture B a une accélération de 4 m/s2 et atteint une vitesse maximale de 40 m/s. Déterminer:
a) Quelle voiture remporte la course?
b) Si après la ligne d'arrivée, au lieu de s'arrêter, les voitures continuaient à rouler, l'une des voitures dépasserait-elle l'autre?
Données du problème:
- Vitesse maximale de la voiture A: vA = 36 m/s;
- Accélération de la voiture A: aA = 5 m/s2;
- Vitesse maximale de la voiture B: vB = 40 m/s;
- Accélération de la voiture B: aB = 4 m/s2.
Nous choisissons un référentil orienté vers la droite avec l'origine au point de départ des voitures. Les vitesses initiales sont dans le même sens que le référentiel.
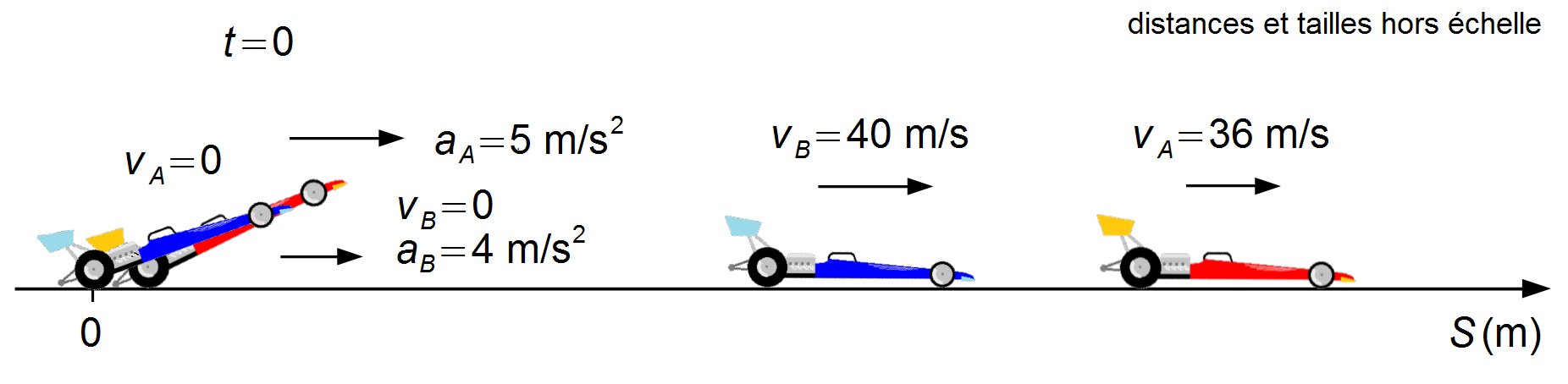
Les voitures partent du repos et accélèrent jusqu'à atteindre leurs vitesses maximales, puis continuent à rouler à des vitesses constantes (Figure 1).
Solution
a) Résolvant en trois parties séparément.
Premièrement, nous devons trouver l'intervalle de temps et la position que chaque voiture a jusqu'à ce qu'elle atteigne sa vitesse maximale. Les voitures accélèrent, elles sont en Mouvement Rectiligne Uniformément Varié la équation horaire de la vitesse est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+at}
\end{gather}
\]
en écrivant cette équation pour chacune des voitures, nous obtenons le temps qu'elles mettent pour passer du
repos à la vitesse maximale
Voiture A:
\[
\begin{gather}
v_{\small A}=v_{0\small A}+a_{\small A}t_{\small A}\\[5pt]
36=0+5t_{\small A}\\[5pt]
t_{\small A}=\frac{36}{5}\\[5pt]
t_{\small A}=7,2\;\mathrm s
\end{gather}
\]
Voiture B:
\[
\begin{gather}
v_{\small B}=v_{0\small B}+a_{\small B}t_{\small B}\\[5pt]
40=0+4t_{\small B}\\[5pt]
t_{\small B}=\frac{40}{4}\\[5pt]
t_{\small B}=10\;\mathrm s
\end{gather}
\]
La équation horaire de la position est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
en écrivant cette équation pour chacune des voitures et en utilisant l'intervalle de temps pendant lequel
elles accélèrent, trouvé ci-dessus, nous obtenons la position qu'elles occupent lorsqu'elles atteignent la
vitesse maximale
Voiture A:
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{0\small A}t_{\small A}+\frac{a_{\small A}}{2}t_{\small A}^2\\[5pt]
S_{\small A}=0+0\times 7,2+\frac{5}{2}\times 7,2^2\\[5pt]
S_{\small A}=2,5\times 51,8\\[5pt]
S_{\small A}=129,6\;\mathrm m
\end{gather}
\]
Voiture B:
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{0\small B}t_{\small B}+\frac{a_{\small B}}{2}t_{\small B}^2\\[5pt]
S_{\small B}=0+0\times10+\frac{4}{2}\times 10^2\\[5pt]
S_{\small B}=2\times100\\[5pt]
S_{\small B}=200\;\mathrm m
\end{gather}
\]
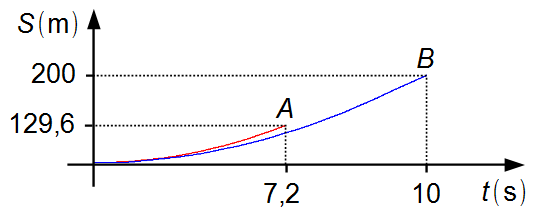
Remarque: jusqu'à l'instant 7,2 s, les deux voitures accélèrent, la voiture A est
devant la voiture B. À partir de cet instant, la voiture A atteint sa vitesse maximale et
commence à se déplacer à vitesse constante, tandis que la voiture B continue d'accélérer jusqu'à
l'instant 10 s (Graphique 1).
Deuxièmement, nous devons trouver la position de la voiture A lorsqu'elle se déplace entre 7,2 s et 10 s avec une vitesse constante, elle est en Mouvement Rectiligne Uniforme, la fonction horaire du mouvement uniforme est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt} \tag{I}
\end{gather}
\]
la position initiale de cette partie du mouvement sera la position trouvée ci-dessus,
S0A = SA = 129,6 m, la vitesse de cette partie du mouvement sera
la vitesse maximale que la voiture atteint, vA = 36 m/s, et l'intervalle de temps sera
tA = 10−7,2 = 2,8 s
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
S_{\small A}=129,6+36\times2,8\\[5pt]
S_{\small A}=229,4\;\mathrm m
\end{gather}
\]
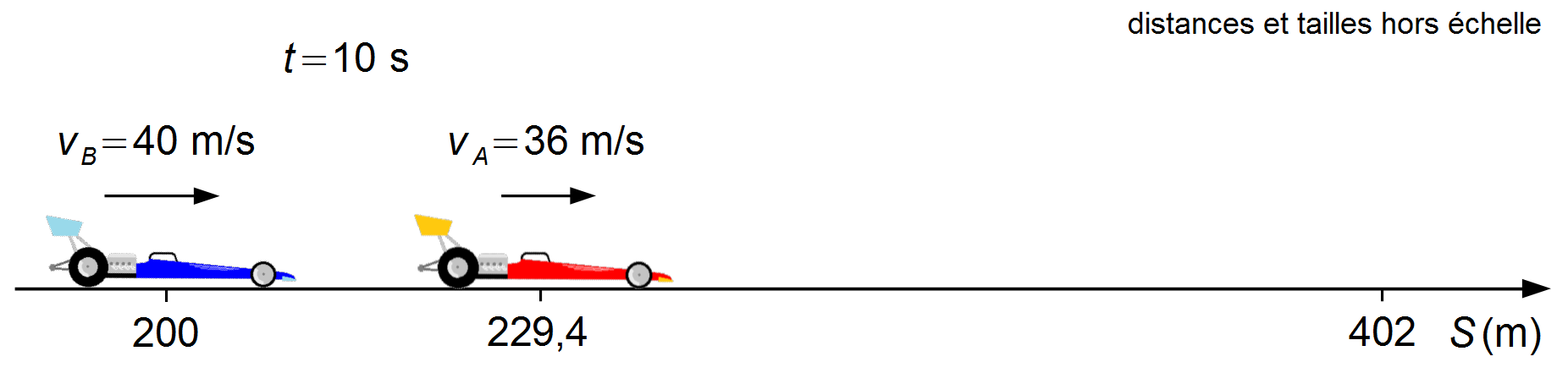
Remarque: entre les instants 7,2 s et 10 s, la voiture A se déplace avec une
vitesse constante donnée par un segment de droite, tandis que la voiture B continue d'accélérer
selon un arc de parabole (Graphique 2). À partir de l'instant 10 s, les deux voitures se déplacent à
vitesse constante, la voiture A devant la voiture B.
Troisièmement, nous devons calculer l'intervalle de temps nécessaire aux voitures pour se déplacer de la position où elles se trouvent à l'instant 10 s jusqu'à la ligne d'arrivée. Les positions des voitures à l'instant 10 s seront la position initiale de chaque voiture pour cette troisième partie, S0A = 229,4 m et S0B = 200 m.
Les voitures courent à des vitesses constantes, en écrivant l'équation (I) pour chacune d'elles
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
402=229,4+36t_{\small A}\\[5pt]
t_{\small A}=\frac{402-229,4}{36}\\[5pt]
t_{\small A}=4,79\;\mathrm s
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t_{\small B}\\[5pt]402=200+40t_{\small B}\\[5pt]
t_{\small B}=\frac{402-200}{40}\\[5pt]
t_{\small B}=5,05\;\mathrm s
\end{gather}
\]
La
voiture A remporte
la course.
Remarque: à partir de l'instant 10 s, les voitures se déplacent à des vitesses constantes, la
voiture A avec une vitesse maximale inférieure à celle de la voiture B,
vA < vB, parvient à franchir la ligne d'arrivée en premier lieu
(Graphique 3).
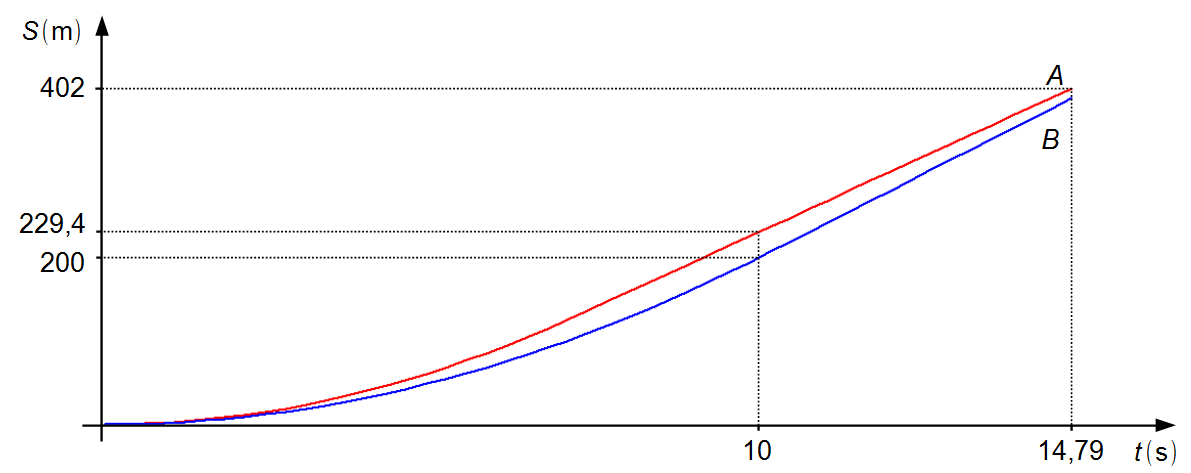Graphique 3
L'intervalle de temps total de la course pour la voiture B est de 15,05 s.
L'intervalle de temps total de la course pour la voiture B est de 15,05 s.
b) À partir de l'instant 10 s, l'équation de mouvement de chacune des voitures, en appliquant l'équation (I), est donnée par
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt]
S_{\small A}=229,4+36t
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t\\[5pt]
S_{\small B}=200+40t
\end{gather}
\]
pour trouver la position où se produit le dépassement, nous devons imposer la condition d'égalité des deux
équations ci-dessus, et trouver l'instant de temps du dépassement
\[
\begin{gather}
S_{A}=S_{\small B}\\[5pt]
229,4+36t=200+40t\\[5pt]
t=\frac{29,4}{4}\\[5pt]
t=7,35\;\mathrm s
\end{gather}
\]
en remplaçant cet instant dans l'équation pour la voiture A (ou B), nous trouvons la position
\[
\begin{gather}
S_{\small A}=229,4+36\times7,35\\[5pt]
S_{\small A}=229,4+264,6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{\small A}=S_{\small B}=494\;\mathrm m}
\end{gather}
\]
Remarque: comme la voiture B a une vitesse plus élevée que la voiture A sur une
distance plus grande, elle dépassera la voiture A. Cela se produit à l'instant 17,35 s après le
début de la course à la position 494 m (Graphique 4).
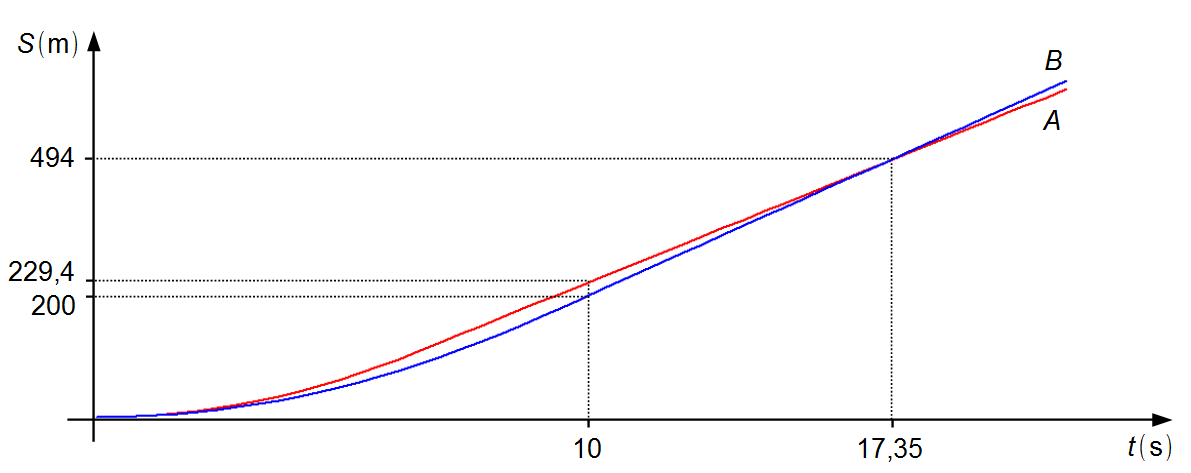Graphique 4
publicité
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .