Solved Problem on One-dimensional Motion
ES
FR
PT-BR
advertisement
Two cars compete in a drag race over a distance of 402 meters (the most common distance for a quarter-mile). The cars start from rest, with car A having an acceleration of 5 m/s2 and reaching a maximum speed of 36 m/s, while car B has an acceleration of 4 m/s2 and reaches a maximum speed of 40 m/s. Determine:
a) Which car wins the race?
b) If after the finish line the cars, instead of stopping, continued running, would one of the cars surpass the other?
Problem data:
- Maximum speed of car A: vA = 36 m/s;
- Acceleration of car A: aA = 5 m/s2;
- Maximum speed of car B: vB = 40 m/s;
- Acceleration of car B: aB = 4 m/s2.
We choose a frame of reference oriented to the right with the origin at the starting point of the cars. The initial velocities are in the same direction as the reference frame.
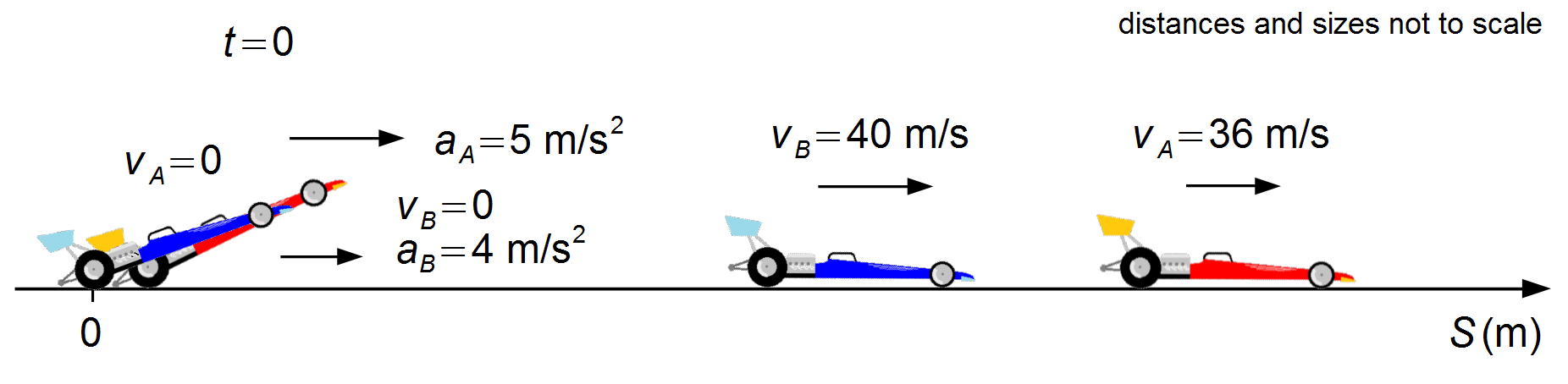
The cars start from rest and accelerate until they reach their maximum velocities, then continue to run at constant velocities (Figure 1).
Solution
a) Solving in three separate parts.
First, we need to find the time interval and the position that each car has until reaching its maximum speed. The cars are accelerating, they are in Uniformly Accelerated Rectlinear Motion, where the equation of velocity as a function of time function is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+at}
\end{gather}
\]
writing this equation for each of the cars, we obtain the time they take to go from rest to maximum speed
Car A:
\[
\begin{gather}
v_{\small A}=v_{0\small A}+a_{\small A}t_{\small A}\\[5pt]
36\;\mathrm{\frac{m}{s}}=0+\left(5\;\mathrm{\frac{m}{s^2}}\right)t_{\small A}\\[5pt]
t_{\small A}=\frac{36\;\mathrm{\frac{\cancel m}{\cancel s}}}{5\;\mathrm{\frac{\cancel m}{s^{\cancel 2}}}}\\[5pt]
t_{\small A}=7.2\;\mathrm s
\end{gather}
\]
Car B:
\[
\begin{gather}
v_{\small B}=v_{0\small B}+a_{\small B}t_{\small B}\\[5pt]
40\;\mathrm{\frac{m}{s}}=0+\left(4\;\mathrm{\frac{m}{s^2}}\right)t_{\small B}\\[5pt]
t_{\small B}=\frac{40\;\mathrm{\frac{\cancel m}{\cancel s}}}{4\;\mathrm{\frac{\cancel m}{s^{\cancel 2}}}}\\[5pt]
t_{\small B}=10\;\mathrm s
\end{gather}
\]
The equation of displacement as a function of time is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
writing this equation for each of the cars and using the time interval in which they accelerate, found above,
we obtain the position they are at when they reach maximum speed
Car A:
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{0\small A}t_{\small A}+\frac{a_{\small A}}{2}t_{\small A}^2\\[5pt]
S_{\small A}=0+0\times\left(7.2\;\mathrm s\right)+\frac{1}{2}\times\left(5\;\mathrm{\frac{m}{s^2}}\right)\left(7.2\;\mathrm s\right)^2\\[5pt]
S_{\small A}=\left(2.5\;\mathrm{\frac{m}{\cancel{s^2}}}\right)\left(51.8\;\mathrm{\cancel{s^2}}\right)\\[5pt]
S_{\small A}=129.6\;\mathrm m
\end{gather}
\]
Car B:
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{0\small B}t_{\small B}+\frac{a_{\small B}}{2}t_{\small B}^2\\[5pt]
S_{\small B}=0+0\times\left(10\;\mathrm s\right)+\frac{1}{2}\times\left(4\;\mathrm{\frac{m}{s^2}}\right)\left(10\;\mathrm s\right)^2\\[5pt]
S_{\small B}=\left(2\;\mathrm{\frac{m}{\cancel{s^2}}}\right)\left(100\;\mathrm{\cancel{s^2}}\right)\\[5pt]
S_{\small B}=200\;\mathrm m
\end{gather}
\]
Note: up to the instant 7.2 s, both cars are accelerating, with car A ahead of
car B. From this instant, car A reaches its maximum speed and begins to move with
constant speed, while car B continues to accelerate until the instant equal to 10 s (Graph 1).
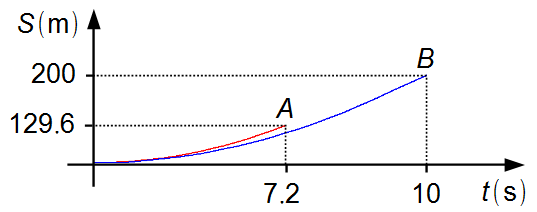
Second, we must find the position of car A when it moves between 7.2 s and 10 s at constant speed, it is in Uniform Rectlinear Motion, where the equation of displacement as a function of times is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt} \tag{I}
\end{gather}
\]
the initial position of this part of the motion will be the position found above,
S0A = SA = 129.6 m, the speed of this part of the motion will
be the maximum speed the car reaches, vA = 36 m/s, and the time interval will be
tA = 10−7.2 = 2.8 s
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
S_{\small A}=129.6\;\mathrm m+\left(36\;\mathrm{\frac{m}{\cancel s}}\right)\left(2,8\;\mathrm{\cancel s }\right)\\[5pt]
S_{\small A}=229.4\;\mathrm m
\end{gather}
\]
Note: between the instants 7.2 s and 10 s, car A moves with constant speed
given by a straight segment, while car B continues to accelerate given by a parabolic arc
(Graph 2). From the instant 10 s onwards, both cars move with constant speed with car A ahead
of car B.
Third, we must calculate the time interval for the cars to move from the position they are in at the instant 10 s to the finish line. The positions where the cars are at the instant 10 s will be the initial position of each car for this third part, S0A = 229.4 m and S0B = 200 m.
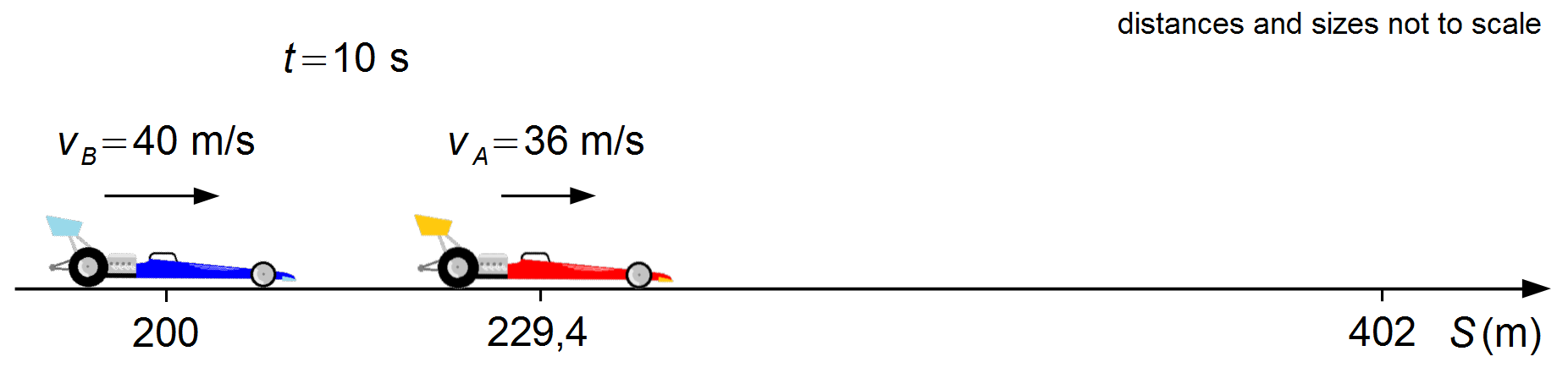
The cars run with constant velocities, writing equation (I) for each of them
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
402\;\mathrm m=229.4\;\mathrm m+\left(36\;\mathrm{\frac{m}{s}}\right)t_{\small A}\\[5pt]
t_{\small A}=\frac{(402-229.4)\;\mathrm{\cancel m}}{36\;\mathrm{\frac{\cancel m}{s}}}\\[5pt]
t_{\small A}=4.79\;\mathrm s
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t_{\small B}\\[5pt]
402=200\;\mathrm m+\left(40\;\mathrm{\frac{m}{s}}\right)t_{\small B}\\[5pt]
t_{\small B}=\frac{(402-200)\;\mathrm{\cancel m}}{40\;\mathrm{\frac{\cancel m}{s}}}\\[5pt]
t_{\small B}=5.05\;\mathrm s
\end{gather}
\]
Car A wins
the race.
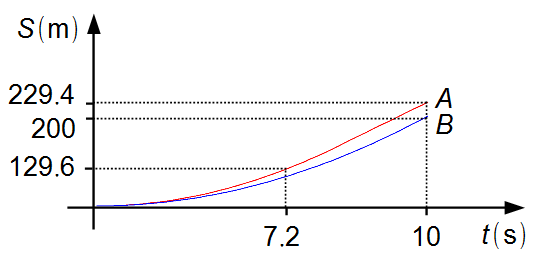
Note: from the instant 10 s onwards, the cars move with constant velocities, with
car A having a maximum speed smaller than car B's,
vA < vB, manages to cross the finish line first (Graph 3).
Graph 3
The total time interval of the race for car B is 15.05 s.
The total time interval of the race for car B is 15.05 s.
b) From the instant 10 s, the motion equation of each of the cars, applying equation (I), is given by
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt]
S_{\small A}=229.4\;\mathrm m+\left(36\;\mathrm{\frac{m}{s}}\right)t
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t\\[5pt]
S_{\small B}=200\;\mathrm m+\left(40\;\mathrm{\frac{m}{s}}\right)t
\end{gather}
\]
to find the position where the overtaking occurs, we must impose the equality condition of the two equations
above and find the instant of time of the overtaking
\[
\begin{gather}
S_{A}=S_{\small B}\\[5pt]
229.4\;\mathrm m+\left(36\;\mathrm{\frac{m}{s}}\right)t=200\;\mathrm m+\left(40\;\mathrm{\frac{m}{s}}\right)t\\[5pt]
t=\frac{29.4\;\mathrm{\cancel m}}{4\;\mathrm{\frac{\cancel m}{s}}}\\[5pt]
t=7.35\;\mathrm s
\end{gather}
\]
substituting this instant in the equation for car A (or B) we find the position
\[
\begin{gather}
S_{\small A}=229.4\;\mathrm m+\left(36\;\mathrm{\frac{m}{\cancel s}}\right)(7.35\;\mathrm{\cancel s})\\[5pt]
S_{\small A}=229.4\;\mathrm m+264.6\;\mathrm m
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{\small A}=S_{\small B}=494\;\mathrm m}
\end{gather}
\]
Note: as car B has a higher speed than car A over a longer distance, it
will overtake car A. This happens at the instant 17.35 s after the start of the race at the
position 494 m (Graph 4).
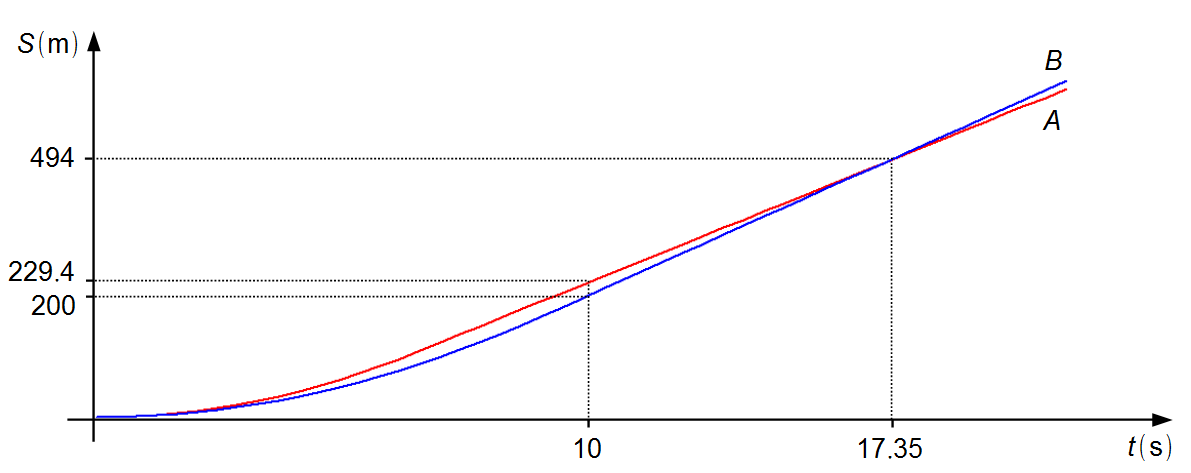Graph 4
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .