Ejercicio Resuelto sobre Movimento Unidimensional
EN
FR
PT-BR
publicidad
Dos coches compiten en una carrera de dragsters en una distancia de 402 m (la distancia más común de ¼ de milla). Los coches parten del reposo; el coche A tiene una aceleración de 5 m/s2 y alcanza una velocidad máxima de 36 m/s, mientras que el coche B tiene una aceleración de 4 m/s2 y alcanza una velocidad máxima de 40 m/s. Determine:
a) ¿Qué coche gana la carrera?
b) Si después de la línea de meta los coches, en lugar de detenerse, continuaran corriendo, ¿uno de los coches adelantaría al otro?
Datos del problema:
- Velocidad máxima del coche A: vA = 36 m/s;
- Aceleración del coche A: aA = 5 m/s2;
- Velocidad máxima del coche B: vB = 40 m/s;
- Aceleración del coche B: aB = 4 m/s2.
Tomamos un sistema de referencia orientado hacia la derecha con origen en el punto de partida de los coches. Las velocidades iniciales están en la misma dirección que el referencial.
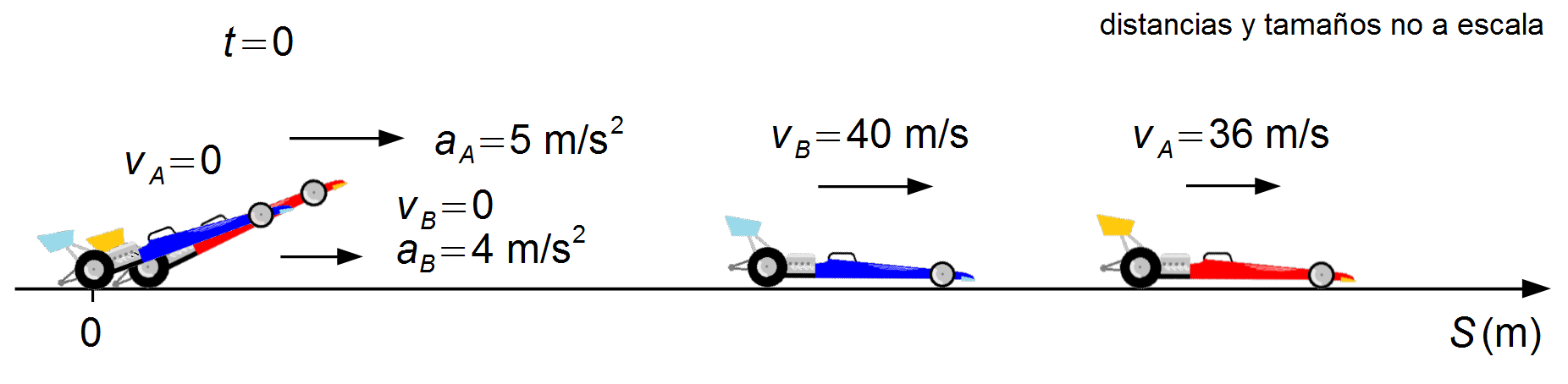
Los coches parten del reposo y aceleran hasta alcanzar sus velocidades máximas, y continúan corriendo con velocidades constantes (Figura 1).
Solución
a) Resolviendo en tres partes separadas.
Primero, debemos encontrar el intervalo de tiempo y la posición que cada coche tiene hasta alcanzar sus velocidades máximas. Los coches están acelerando, están en Movimiento Rectilíneo Uniformemente Variado (MRUV). La función horaria de la velocidad está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+at}
\end{gather}
\]
escribiendo esta ecuación para cada uno de los coches, obtenemos el tiempo que llevan desde el reposo hasta
la velocidad máxima
Coche A:
\[
\begin{gather}
v_{\small A}=v_{0\small A}+a_{\small A}t_{\small A}\\[5pt]
36=0+5t_{\small A}\\[5pt]
t_{\small A}=\frac{36}{5}\\[5pt]
t_{\small A}=7,2\;\mathrm s
\end{gather}
\]
Coche B:
\[
\begin{gather}
v_{\small B}=v_{0\small B}+a_{\small B}t_{\small B}\\[5pt]
40=0+4t_{\small B}\\[5pt]
t_{\small B}=\frac{40}{4}\\[5pt]
t_{\small B}=10\;\mathrm s
\end{gather}
\]
Ecuación de la posición en función del tiempo
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
escribiendo esta ecuación para cada uno de los coches y usando el intervalo de tiempo en el que aceleran,
encontrado arriba, obtenemos la posición en la que están cuando alcanzan la velocidad máxima
Coche A:
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{0\small A}t_{\small A}+\frac{a_{\small A}}{2}t_{\small A}^2\\[5pt]
S_{\small A}=0+0\times 7,2+\frac{5}{2}\times 7,2^2\\[5pt]
S_{\small A}=2,5\times 51,8\\[5pt]
S_{\small A}=129,6\;\mathrm m
\end{gather}
\]
Coche B:
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{0\small B}t_{\small B}+\frac{a_{\small B}}{2}t_{\small B}^2\\[5pt]
S_{\small B}=0+0\times10+\frac{4}{2}\times 10^2\\[5pt]
S_{\small B}=2\times100\\[5pt]
S_{\small B}=200\;\mathrm m
\end{gather}
\]
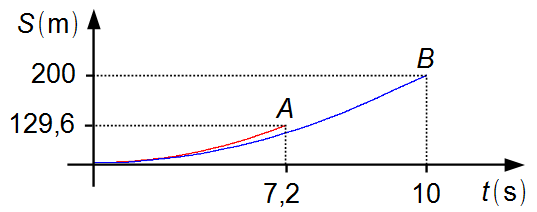
Observación: hasta el instante 7,2 s ambos los coches están acelerando, el coche A
está delante del coche B. A partir de ese instante, el coche A alcanza su velocidad
máxima y comienza a moverse con velocidad constante, mientras que el coche B continúa acelerando
hasta el instante igual a 10 s (Gráfico 1).
Segundo, debemos encontrar la posición del coche A cuando se desplaza entre 7,2 s y 10 s con velocidad constante, está en Movimiento Rectilíneo Uniforme (MRU), la ecuación del movimiento uniforme está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt} \tag{I}
\end{gather}
\]
la posición inicial de esta parte del movimiento será la posición encontrada anteriormente,
S0A = SA = 129,6 m, la velocidad de esta parte del movimiento será
la velocidad máxima que alcanza el coche, vA = 36 m/s, y el intervalo de tiempo será
tA = 10−7,2 = 2,8 s
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
S_{\small A}=129,6+36\times2,8\\[5pt]
S_{\small A}=229,4\;\mathrm m
\end{gather}
\]
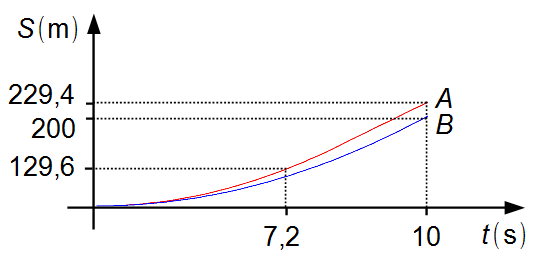
Observación: entre los instantes 7,2 s y 10 s, el coche A se mueve con velocidad
constante dada por un segmento de recta, mientras que el coche B continúa acelerando,
representado por un arco de parábola (Gráfico 2). A partir del instante 10 s, ambos los coches se
desplazan con velocidad constante, con el coche A delante del coche B.
Tercero, debemos calcular el intervalo de tiempo para que los coches se desplacen desde la posición en la que se encuentran en el instante 10 s hasta la línea de meta. Las posiciones en las que se encuentran los coches en el instante 10 s serán la posición inicial de cada coche para esta tercera parte, S0A = 229,4 m y S0B = 200 m.
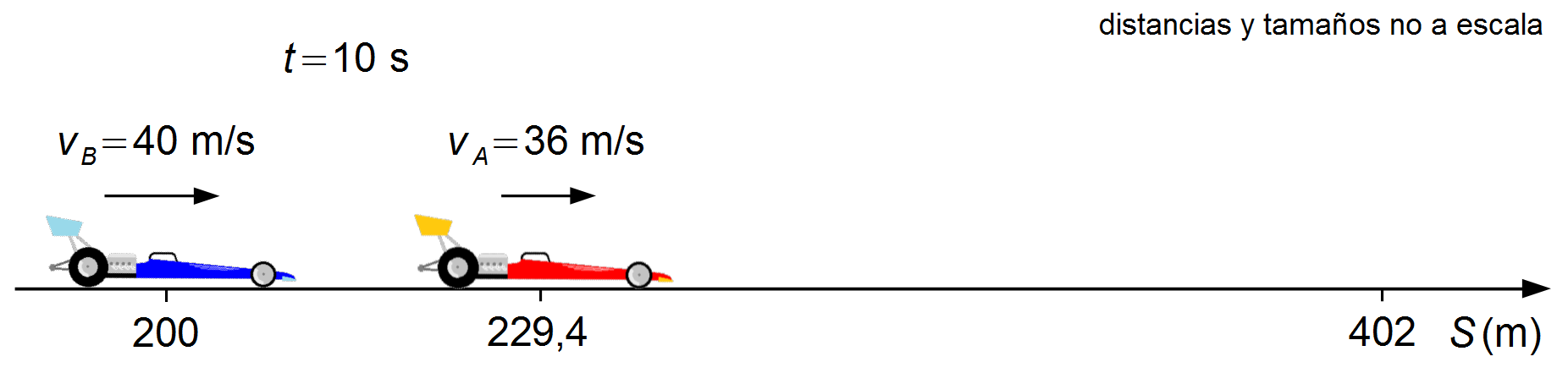
Los coches corren con velocidades constantes, escribiendo la ecuación (I) para cada uno de ellos.
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
402=229,4+36t_{\small A}\\[5pt]
t_{\small A}=\frac{402-229,4}{36}\\[5pt]
t_{\small A}=4,79\;\mathrm s
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t_{\small B}\\[5pt]402=200+40t_{\small B}\\[5pt]
t_{\small B}=\frac{402-200}{40}\\[5pt]
t_{\small B}=5,05\;\mathrm s
\end{gather}
\]
El
coche A gana
la carrera.
Observación: a partir del instante 10 s, los coches se desplazan con velocidades constantes,
el coche A con velocidad máxima menor que la velocidad del coche B,
vA < vB, logra cruzar la línea de llegada en primer lugar
(Gráfico 3).
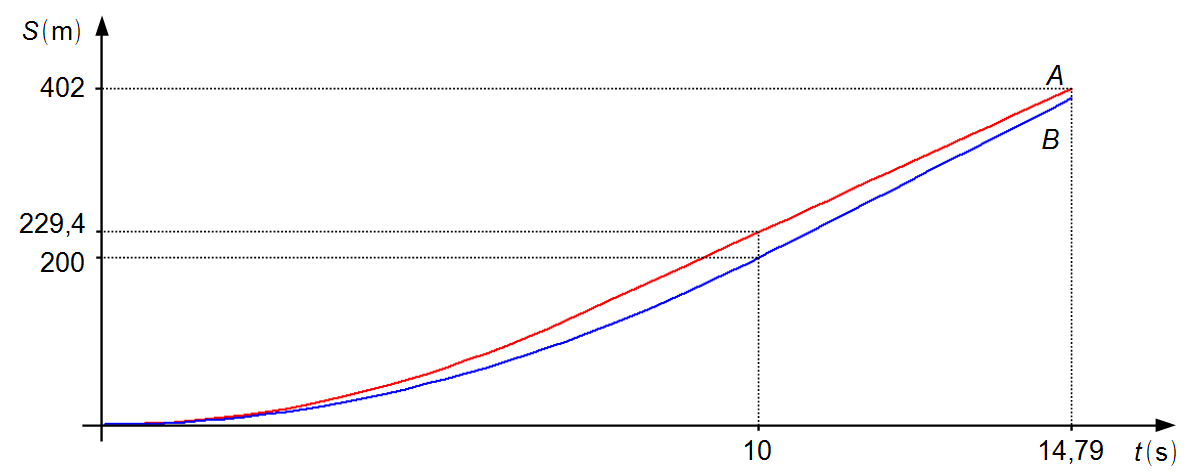Gráfico 3
El tiempo total de la carrera para el coche B es de 15,05 s.
El tiempo total de la carrera para el coche B es de 15,05 s.
b) A partir del instante 10 s, la ecuación de movimiento de cada uno de los coches, aplicando la ecuación (I), se da por
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt]
S_{\small A}=229,4+36t
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t\\[5pt]
S_{\small B}=200+40t
\end{gather}
\]
para encontrar la posición en la que ocurre el adelantamiento, debemos imponer la condición de igualdad de
las dos ecuaciones anteriores y encontrar el instante de tiempo del adelantamiento
\[
\begin{gather}
S_{A}=S_{\small B}\\[5pt]
229,4+36t=200+40t\\[5pt]
t=\frac{29,4}{4}\\[5pt]
t=7,35\;\mathrm s
\end{gather}
\]
sustituyendo este instante en la ecuación para el coche A (o B) encontramos la posición
\[
\begin{gather}
S_{\small A}=229,4+36\times7,35\\[5pt]
S_{\small A}=229,4+264,6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{\small A}=S_{\small B}=494\;\mathrm m}
\end{gather}
\]
Observación: como el coche B tiene una velocidad mayor que el coche A en una
distancia mayor, adelantará al coche A. Esto ocurre en el instante 17,35 s después del inicio de la
carrera en la posición 494 m (Gráfico 4).
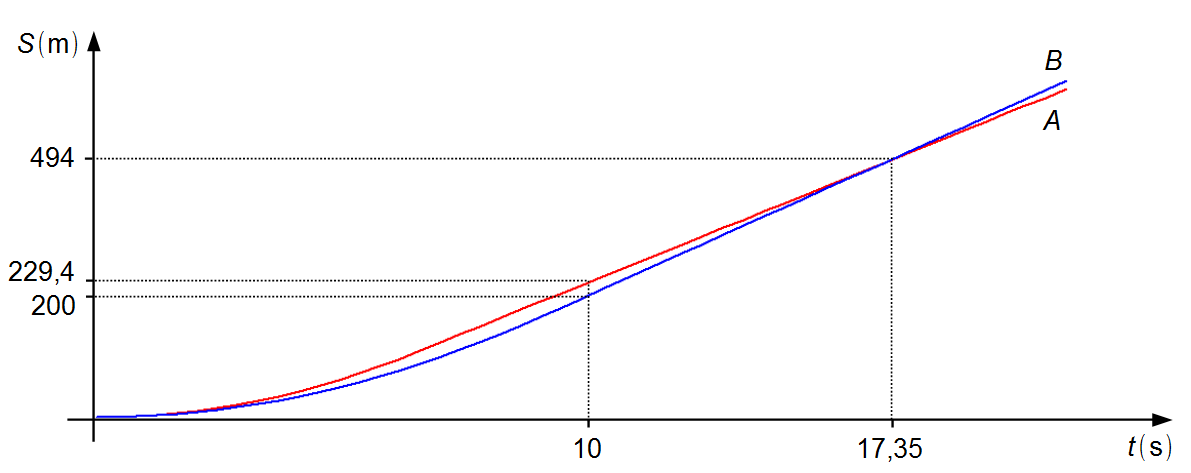Gráfico 4
publicidad
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .