Exercício Resolvido de Movimento Unidimensional
publicidade
Dois carros disputam uma corrida de dragsters em uma distância de 402 m (distância mais comum de ¼ de milha). Os carros partem do repouso, o carro A possui uma aceleração de 5 m/s2 e atinge uma velocidade máxima de 36 m/s, o carro B possui uma aceleração de 4 m/s2 e atinge uma velocidade máxima de 40 m/s. Determine:
a) Qual carro ganha a corrida?
b) Se após a linha de chegada os carros, ao invés de parar, continuassem correndo um dos carros ultrapassaria o outro?
Dados do problema:
- Velocidade máxima do carro A: vA = 36 m/s;
- Aceleração do carro A: aA = 5 m/s2;
- Velocidade máxima do carro B: vB = 40 m/s;
- Aceleração do carro B: aB = 4 m/s2.
Adotamos um sistema de referência orientado para a direita com origem no ponto largada dos carros. As velocidades iniciais estão no mesmo sentido do referencial.
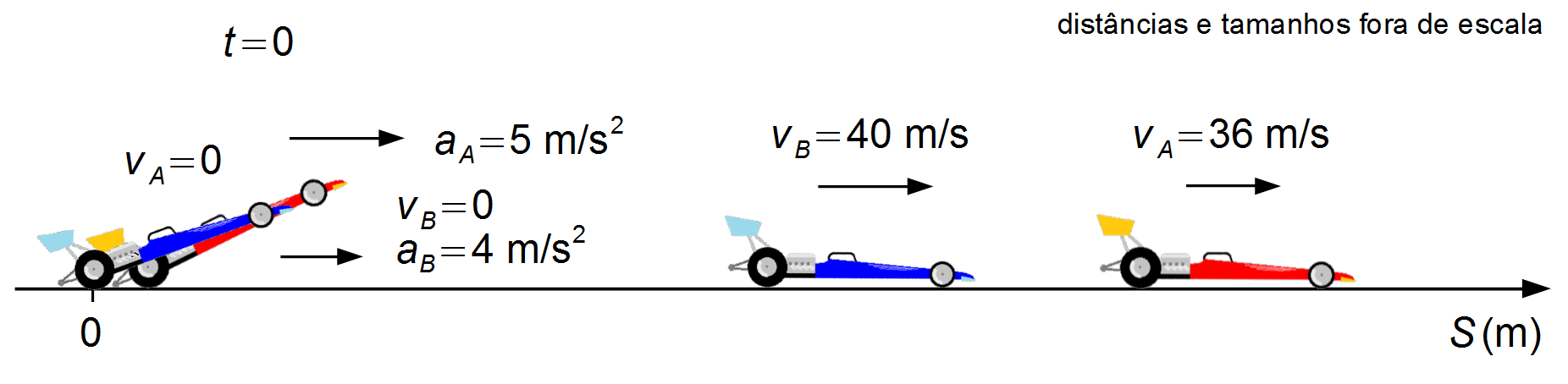
Os carros partem do repouso e aceleram até atingir suas velocidades máximas, e continuam a correr com velocidades constantes (Figura 1).
Solução
a) Resolvendo em três partes separadamente.
Primeiro, devemos encontrar o intervalo de tempo e a posição que cada carro tem até atingir suas velocidades máximas. Os carros estão acelerando, estão em Movimento Retilíneo Uniformemente Variado (M.R.U.V.) a função horária da velocidade é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+at}
\end{gather}
\]
escrevendo esta equação para cara um dos carros obtemos o tempo que eles levam para ir do repouso até a
velocidade máxima
Carro A:
\[
\begin{gather}
v_{\small A}=v_{0\small A}+a_{\small A}t_{\small A}\\[5pt]
36=0+5t_{\small A}\\[5pt]
t_{\small A}=\frac{36}{5}\\[5pt]
t_{\small A}=7,2\;\mathrm s
\end{gather}
\]
Carro B:
\[
\begin{gather}
v_{\small B}=v_{0\small B}+a_{\small B}t_{\small B}\\[5pt]
40=0+4t_{\small B}\\[5pt]
t_{\small B}=\frac{40}{4}\\[5pt]
t_{\small B}=10\;\mathrm s
\end{gather}
\]
A função horária da posição é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
escrevendo esta equação para cara um dos carros e usando o intervalo de tempo em que eles acelera, encontrado
acima, obtemos a posição que eles estão quando atingem a velocidade máxima
Carro A:
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{0\small A}t_{\small A}+\frac{a_{\small A}}{2}t_{\small A}^2\\[5pt]
S_{\small A}=0+0\times 7,2+\frac{5}{2}\times 7,2^2\\[5pt]
S_{\small A}=2,5\times 51,8\\[5pt]
S_{\small A}=129,6\;\mathrm m
\end{gather}
\]
Carro B:
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{0\small B}t_{\small B}+\frac{a_{\small B}}{2}t_{\small B}^2\\[5pt]
S_{\small B}=0+0\times10+\frac{4}{2}\times 10^2\\[5pt]
S_{\small B}=2\times100\\[5pt]
S_{\small B}=200\;\mathrm m
\end{gather}
\]
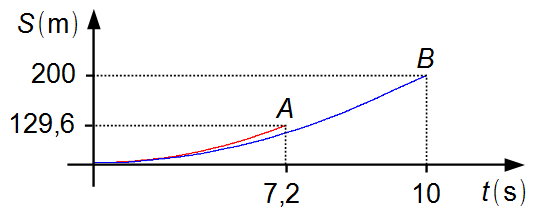
Observação: até o instante 7,2 s ambos os carros estão acelerando, o carro A está
na frente do carro B. A partir desse instante o carro A atinge sua velocidade máxima e
começa a se mover com velocidade constante, enquanto o carro B continua a acelerar até o
instante igual a 10 s (Gráfico 1).
Segundo, devemos encontrar a posição do carro A quando ele se desloca entre 7,2 s e 10 s com velocidade constante, ele está em Movimento Retilíneo Uniforme (M.R.U.), a função horária do movimento uniforme é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt} \tag{I}
\end{gather}
\]
a posição inicial desta parte do movimento será a posição encontrada acima,
S0A = SA = 129,6 m, a velocidade desta parte do movimento será a
velocidade máxima que o carro atinge, vA = 36 m/s, e o intervalo de tempo será
tA = 10−7,2 = 2,8 s
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
S_{\small A}=129,6+36\times2,8\\[5pt]
S_{\small A}=229,4\;\mathrm m
\end{gather}
\]
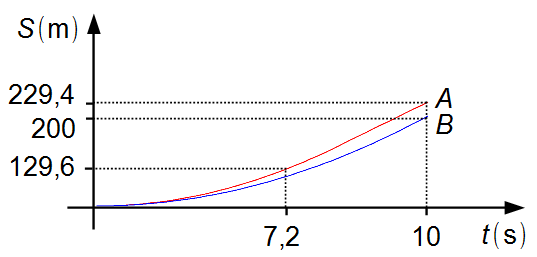
Observação: entre os instantes 7,2 s e 10 s o carro A se move com velocidade
constante dado por um segmento de reta, enquanto o carro B continua acelerando dado por um arco de
parábola (Gráfico 2). A partir do instante 10 s ambos os carros se deslocam com velocidade constante
com o carro A a frente do carro B.
Terceiro, devemos calcular o intervalo de tempo para os carros se deslocarem da posição em que se encontram no instante 10 s até a linha de chegada. As posições em que os carros se encontram no instante 10 s será a posição inicial de cada carro para essa terceira parte, S0A = 229,4 m e S0B = 200 m.

Os carros correm com velocidades constantes, escrevendo a equação (I) para cada um deles
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t_{\small A}\\[5pt]
402=229,4+36t_{\small A}\\[5pt]
t_{\small A}=\frac{402-229,4}{36}\\[5pt]
t_{\small A}=4,79\;\mathrm s
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t_{\small B}\\[5pt]402=200+40t_{\small B}\\[5pt]
t_{\small B}=\frac{402-200}{40}\\[5pt]
t_{\small B}=5,05\;\mathrm s
\end{gather}
\]
O
carro A ganha
a corrida.
Observação: a partir do instante 10 s os carros se deslocam com velocidades constantes, o
carro A com velocidade máxima menor do que a velocidade do carro B,
vA < vB, consegue cruzar a linha de chegada em primeiro lugar
(Gráfico 3).
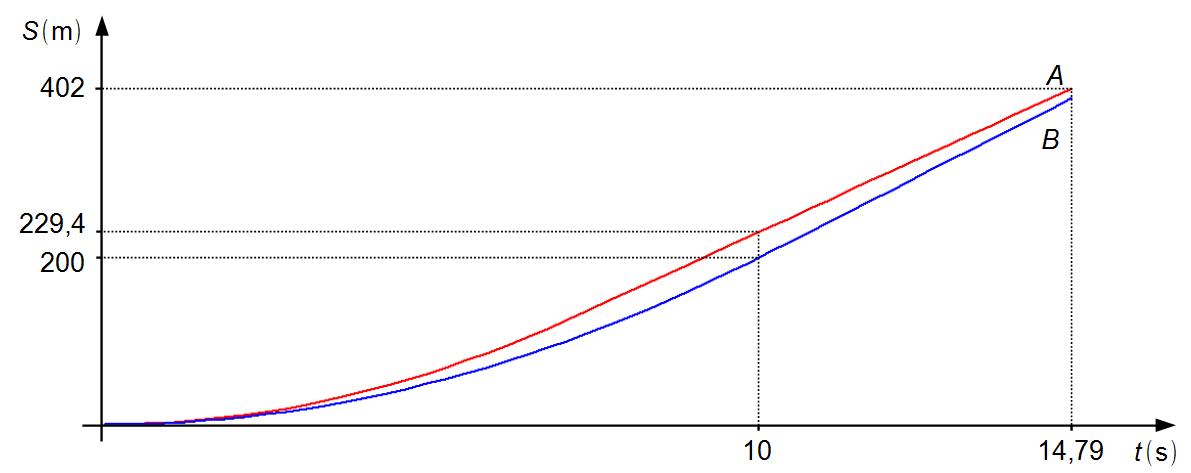 Gráfico 3
Gráfico 3
O intervalo de tempo total da corrida para o carro B é de 15,05 s.

O intervalo de tempo total da corrida para o carro B é de 15,05 s.
b) A partir do instante 10 s a equação de movimento de cada um dos carros, aplicando a equação (I), é dada por
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt]
S_{\small A}=229,4+36t
\end{gather}
\]
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{\small B}t\\[5pt]
S_{\small B}=200+40t
\end{gather}
\]
para encontrarmos a posição em que ocorre a ultrapassagem devemos impor a condição de igualdade das duas
equações acima, e encontrar o instante de tempo da ultrapassagem
\[
\begin{gather}
S_{A}=S_{\small B}\\[5pt]
229,4+36t=200+40t\\[5pt]
t=\frac{29,4}{4}\\[5pt]
t=7,35\;\mathrm s
\end{gather}
\]
substituindo esse instante na equação para o carro A (ou B) encontramos a posição
\[
\begin{gather}
S_{\small A}=229,4+36\times7,35\\[5pt]
S_{\small A}=229,4+264,6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{\small A}=S_{\small B}=494\;\mathrm m}
\end{gather}
\]
Observação: como o carro B tem velocidade maior do que o carro A em uma
distância maior ele ultrapassará o carro A. Isto acontece no instante 17,35 s após o início da
corrida na posição 494 m (Gráfico 4).
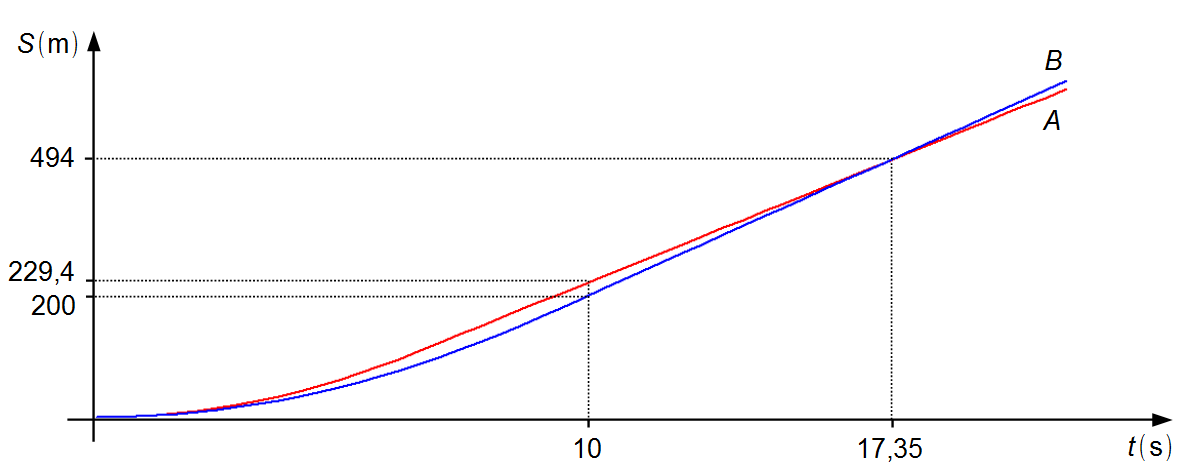 Gráfico 4
Gráfico 4

publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .