Un projectile est tiré avec une vitesse initiale v₀ et formant un angle θ₀ avec l'horizontale, en sachant que les points de tir et la cible sont sur le même plan horizontal et en négligeant la résistance de l'air, déterminer:
a) La hauteur maximale atteinte par le projectile;
b) Le temps nécessaire pour atteindre la hauteur maximale;
c) Le temps total de durée du mouvement;
d) La portée maximale horizontale du projectile;
e) L'équation de la trajectoire du mouvement du projectile;
f) L'angle de tir qui permet d'obtenir la portée maximale;
g) Démontrer que des tirs avec des angles complémentaires ont la même portée;
h) La vitesse en un point quelconque de la trajectoire;
i) Les composantes de l'accélération en un point quelconque de la trajectoire.


Données du problème:

• Vitesse initiale:    v₀;
• Angle de tir par rapport à l'horizontale:    θ₀.

Schéma du problème:

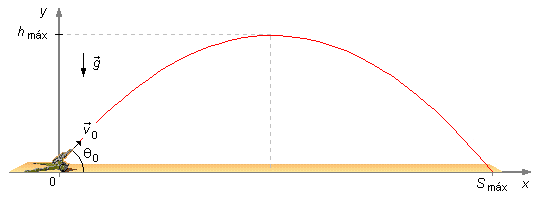
Nous choisissons un referentiel avec l'axe Ox pointant vers la droite et Oy vers le haut, l'accélération de la pesanteur pointant vers le bas et le point de tir étant à l'origine du référentiel (x₀, y₀) = (0, 0), (Figure 1).


Solution

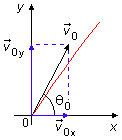
Le mouvement peut être décomposé le long des axes x et y. Les composantes de la vitesse initiale v₀ sont données en module par (Figure 2)
dans le mouvement uniforme, v_x = v_0x est constant, nous pouvons substituer v_x par la valeur de (I) et S_0x = 0 Dans la direction y, le projectile est soumis à l'accélération de la pesanteur, c'est un Mouvement Rectiligne Uniformément Varié, représenté par un lancement vers haut pendant la montée et une chute libre lors de la descente, où S_0y = 0, v_0y est donnée par l'expression (II) et a = −g est l'accélération de la pesanteur qui est opposée à l'orientation de la trajectoire. 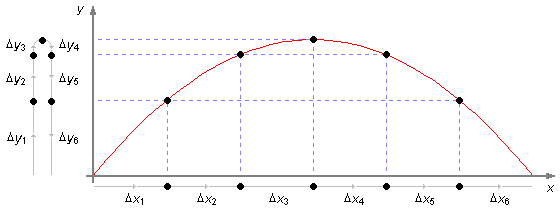l'équation de la vitesse est donnée par l'équation de la vitesse en fonction de l'accélération et du déplacement est donnée par Dans la Figure 3, nous voyons que dans le mouvement le long de la direction x, pour des intervalles de temps égaux, nous avons des déplacements égaux (Δx₁ = Δx₂ = Δx₃ = Δx₄ = Δx₅ = Δx₆). Dans la direction y, pendant la montée, pour des intervalles de temps égaux, nous avons des déplacements plus petits, la particule est freinée par l'action de la gravité (Δy₁ > Δy₂ > Δy₃), jusqu'à ce que la vitesse v_y soit nulle. Pendant la descente, la gravité commence à ramener la particule au sol avec une vitesse accélérée, pour des intervalles de temps égaux, nous avons des dẽplacements de plus en plus grands (Δy₄ < Δy₅ < Δy₆).


a) Pour trouver la hauteur maximale, h_max, atteinte par le projectile, nous analysons le mouvement le long de la direction y. Lorsque le projectile atteint la hauteur maximale, sa vitesse v_y devient nulle, v_y = 0, en utilisant l'équation (VI)
b) Le temps de montée, t_M, pour atteindre la hauteur maximale sera obtenu à partir de l'équation (V) avec la condition que la vitesse soit nulle à la hauteur maximale atteinte par le projectile, v_y = 0
c) Le temps total, t_T, du mouvement sera la somme des temps de montée, t_M, et de descente, t_D, sachant que dans le mouvement de lancement vertical et de chute libre, les temps de montée et de descente sont égaux. Nous avons donc la condition avec t_M = t_D en utilisant le résultat pour le temps de montée obtenu dans l'élément précédent
d) Le temps calculé ci-dessus, pour que le projectile monte et descende, est également le temps qu'il mettra pour aller de l'origine jusqu'au point S_max le long de l'axe des x, en remplaçant la réponse de l'élément précédent dans l'équation (III)
et en substituant cette identité dans l'équation ci-dessus, nous obtenons la portée maximale
e) Pour obtenir l'équation de la trajectoire, indiquée dans la Figure 1, nous devons avoir y comme fonction de x, ou y = f(x), en utilisant les équations (III) et (IV) pour les mouvements en x et y et en se rappelant que S_0x = S_0y = 0, nous avons le système suivant en isolant le temps dans la première équation en substituant cette valeur dans la deuxième équation En faisant l'association montrée ci-dessous avec une Équation du Second Degré du type y = ax²+bx+c nous voyons que nous avons obtenu une fonction du type S_y = f(S_x) avec le coefficient a < 0, ce qui indique que notre trajectoire est une parabole tournée vers le bas.

f) La réponse obtenue dans l'article (d) pour la portée maximale, S_max, dépend de l'angle initial de lancement. De la trigonométrie, nous savons que la fonction sinus varie de −1 à 1. La valeur maximale de la portée se produit lorsque


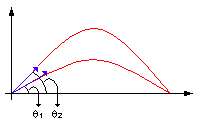
g) En trigonométrie, nous savons que les angles complémentaires sont ceux dont la somme est égale à 90° ou \( \frac{\pi}{2} \), deux angles θ₁ et θ₂ sont complémentaires
En écrivant l'expression (VII) de θ₂ en fonction de θ₁ et en substituant dans l'équation (IX) étant donné \( \operatorname{sen}\pi=0 \), \( \cos\pi=-1 \) en comparant les équations (VIII) et (X)


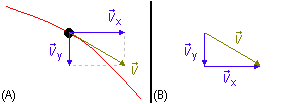
Dans la Figure 5-B, nous voyons que les vecteurs forment un triangle rectangle et le module de la vitesse peut être calculé en appliquant le Théorème de Pythagore en utilisant v_x = v_0x de l'expression (I), et v_y de l'équation (V) dans les deux premiers termes du côté droit de l'égalité, nous factorisant \( v_0^2 \) et dans les troisième et quatrième termes, factorisant −2g
dans le premier terme entre parenthèses, nous appliquons la relation trigonométrique ci-dessus, le deuxième terme entre parenthèses peut être obtenu à partir de l'équation (IV) de la position dans la direction y avec S₀ = S_0y étant donné \( \Delta S_y=S_y-S_{0y} \),, ainsi l'équation (XII) peut être écrite
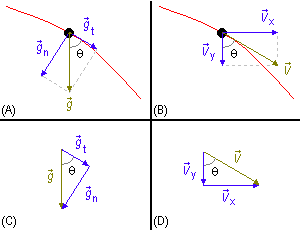
i) L'accélération de la pesanteur, \( \vec g \), à laquelle le projectile est soumis à n'importe quel point de la trajectoire peut être décomposée en accélération tangentielle, \( {\vec g}_t \), et en accélération normale, \( {\vec g}_n \), qui est perpendiculaire à la trajectoire au point considéré (Figure 6-A). De la Figure 6-C
en substituant cette valeur du cosinus dans l'expression (XIII), l'accélération tangentielle sera De même que dans la Figure 6-D et en substituant dans l'expression (XIV) pour l'accélération normale