Un proyectil es disparado con velocidad inicial igual a v₀ y formando un ángulo θ₀ con la horizontal, sabiendo que los puntos de disparo y el objetivo están en el mismo plano horizontal y despreciando la resistencia del aire, determine:
a) La altura máxima que alcanza el proyectil;
b) El tiempo necesario para alcanzar la altura máxima;
c) El tiempo de duración del movimiento total;
d) El alcance máximo horizontal del proyectil;
e) La ecuación de la trayectoria del movimiento del proyectil;
f) El ángulo de tiro que proporciona el máximo alcance;
g) Demostrar que los disparos con ángulos complementarios tienen el mismo alcance;
h) La velocidad en cualquier punto de la trayectoria;
i) Las componentes de la aceleración en cualquier punto de la trayectoria.


Datos del problema:

• Velocidad inicial:    v₀;
• Ángulo de tiro con la horizontal:    θ₀.

Esquema del problema:

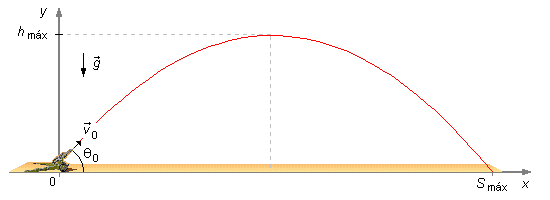
Tomamos un sistema de referencia con el eje Ox apuntando hacia la derecha y Oy hacia arriba, la aceleración de la gravedad está apuntando hacia abajo y el punto de disparo está en el origen del referencial (x₀, y₀) = (0, 0) (Figura 1).


Solución

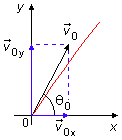
El movimiento puede ser proyectado a lo largo de los ejes x e y. Las componentes de la velocidad inicial v₀ se dan en módulo por (Figura 2)
en el movimiento uniforme, v_x = v_0x es constante, podemos sustituir v_x por el valor de (I) y S_0x = 0 En la dirección y, el proyectil está bajo la acción de la aceleración de la gravedad, es un Movimiento Uniformemente Variado (MUV), representado por un lanzamiento vertical durante la subida y una caída libre en la bajada, donde S_0y = 0, v_0y está dada por la expresión (II) y a = −g es la aceleración de la gravedad que está en dirección opuesta a la orientación de la trayectoria. 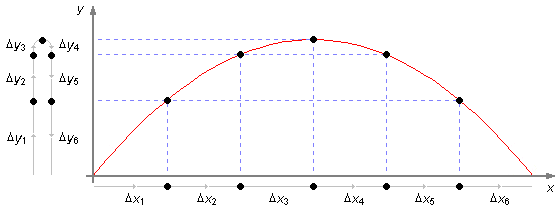La ecuación de la velocidad es dada por La ecuación de la velocidad en función de la aceleración y del desplazamiento es dada por En la Figura 3 vemos que en el movimiento a lo largo de la dirección x, para intervalos de tiempos iguales, tenemos desplazamientos iguales (Δx₁ = Δx₂ = Δx₃ = Δx₄ = Δx₅ = Δx₆).. En la dirección y, durante la ascensión, para intervalos de tiempos iguales, tenemos desplazamientos menores, la partícula está siendo frenada por la acción de la gravedad (Δy₁ > Δy₂ > Δy₃), hasta que la velocidad v_y se iguala a cero. Durante la caída, la gravedad comienza a jalar la partícula de vuelta al suelo con velocidad acelerada, para intervalos de tiempos iguales, tenemos desplazamientos cada vez mayores (Δy₄ < Δy₅ < Δy₆).


a) Para encontrar la altura máxima, h_max, alcanzada por el proyectil, analizamos el movimiento a lo largo de la dirección y. Cuando el proyectil alcanza la altura máxima, su velocidad vy se iguala a cero, v_y = 0, utilizando la ecuación (VI)
b) El tiempo de ascenso, t_A, para alcanzar la altura máxima se obtendrá de la ecuación (V) con la condición de que la velocidad se iguala a cero en la altura máxima alcanzada por el proyectil, v_y = 0
c) El tiempo total, t_T, del movimiento será la suma de los tiempos de ascenso, t_A, y de descenso, t_D, siendo que en el movimiento de lanzamiento vertical y caída libre los tiempos de ascenso y de descenso son iguales, tenemos la condición con t_A = t_D utilizando el resultado para el tiempo de ascenso obtenido en el ítem anterior
d) El tiempo calculado anteriormente, para que el proyectil suba y baje, también es el tiempo que llevará para ir desde el origen hasta el punto S_max a lo largo del eje x, sustituyendo la respuesta del ítem anterior en la ecuación (III)
y sustituyendo esta identidad en la ecuación anterior, obtenemos el alcance máximo
e) Para obtener la ecuación de la trayectoria, indicada en la Figura 1, necesitamos tener y como función de x, o y = f(x), utilizando las ecuaciones (III) y (IV) para los movimientos en x e y recordando que S_0x = S_0y = 0, tenemos el sistema aislando el tiempo en la primera ecuación sustituyendo este valor en la segunda ecuación Haciendo la asociación mostrada abajo con una Ecuación de Segundo Grado del tipo y = ax²+bx+c vemos que hemos obtenido una función del tipo S_y = f(S_x) con el coeficiente a < 0 lo que indica que nuestra trayectoria es una parábola con la "boca" hacia abajo.

f) La respuesta obtenida en el ítem (d) para el alcance máximo, S_max, depende del ángulo inicial de lanzamiento, de trigonometría sabemos que la función seno varía de −1 a 1, el valor máximo del alcance ocurre cuando


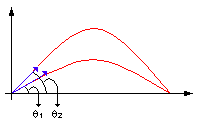
g) En trigonometría, tenemos que los ángulos complementarios son aquellos que suman 90° o \( \frac{\pi}{2} \), dos ángulos θ₁ y θ₂ complementarios
Escribiendo la expresión (VII) de θ₂ en función de θ₁ y sustituyendo en la ecuación (IX) siendo \( \operatorname{sen}\pi=0 \), \( \cos\pi=-1 \) comparando las ecuaciones (VIII) y (X)


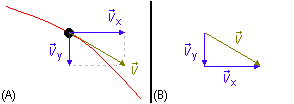
En la Figura 5-B vemos que los vectores forman un triángulo rectángulo y el módulo de la velocidad puede ser calculado aplicando el Teorema de Pitágoras utilizando v_x = v_0x de la expresión (I), y v_y de la ecuación (V) en los dos primeros términos del lado derecho de la igualdad factorizamos \( v_0^2 \) y en el tercer y cuarto términos factorizamos −2g
en el primer término entre paréntesis aplicamos la identidad trigonométrica arriba, el segundo término entre paréntesis puede ser obtenido de la ecuación (IV) de la posición en la dirección y con S₀ = S_0y siendo \( \Delta S_y=S_y-S_{0y} \), así la ecuación (XII) puede ser escrita
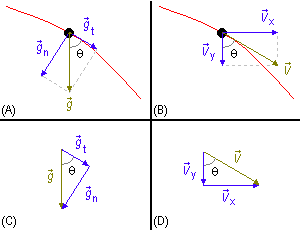
i) La aceleración de la gravedad, \( \vec g \), a la que está sujeto el proyectil en cualquier punto de la trayectoria se puede proyectar en la aceleración tangencial, \( {\vec g}_t \), y en la aceleración normal, \( {\vec g}_n \), que es perpendicular a la trayectoria en el punto considerado (Figura 6-A). De la Figura 6-C
sustituyendo este valor del coseno en la expresión (XIII), la aceleración tangencial será De la misma forma de la Figura 6-D y sustituyendo en la expresión (XIV) para la aceleración normal