Exercice Résolu sur les Mouvement Bidimensionnel
publicité
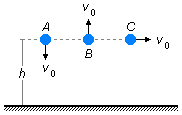
Trois sphères identiques sont lancées d'une même hauteur h avec des vitesses de même module. La
sphère A est lancée verticalement vers le bas, B est lancée verticalement vers le haut et
C est lancée horizontalement. Laquelle d'entre elles atteint le sol avec la plus grande vitesse
en module, en négligeant la résistance de l'air.
Données du problème:
- Vitesse de lancement: v0;
- Hauteur du point de lancement: h.
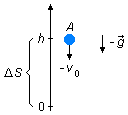
- Sphère A:
\[
\begin {gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2+2a\Delta S} \tag{I}
\end{gather}
\]
\[
\begin{gather}
v^2=(-v_0)^2+2(-g)\Delta S\\[5pt]
v^2=v_0^2-2g(0-h)\\[5pt]
v^2=v_0^2-2g(-h)\\[5pt]
v^2=v_0^2+2gh\\[5pt]
v=\sqrt{v_0^2+2gh} \tag{II}
\end{gather}
\]
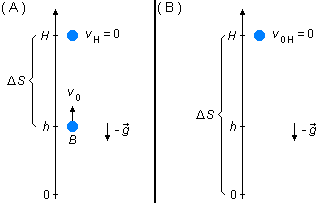
- Sphère B:
Dans la première partie, la vitesse initiale de lancement est positive, elle est orientée dans le même sens que le référentiel, et la vitesse finale est nulle, vH = 0, c'est l'instant où la sphère s'arrête et inverse son mouvement pour commencer à tomber (Figure 2-A).
En écrivant l'équation (I) pour la première partie, nous trouvons la hauteur atteinte par la sphère
\[
\begin{gather}
v^2=v_0^2+2a\Delta S\\[5pt]
v_H^2=v_0^2+2(-g)\Delta S\\[5pt]
0^2=v_0^2-2g(H-h)\\[5pt]
0=v_0^2-2gH+2gh\\[5pt]
2gH=v_0^2+2gh\\[5pt]
H=\frac{v_0^2+2gh}{2g} \tag{III}
\end{gather}
\]
Dans la seconde partie, chute libre, la vitesse initiale sera la vitesse finale de la première partie, elle
sera nulle, v0H = vH = 0, et la hauteur initiale sera donnée par
l'équation (III). En appliquant l'équation (I), nous obtenons la vitesse avec laquelle la sphère atteint
le sol
\[
\begin{gather}
v^2=v_0^2+2a\Delta S\\[5pt]
v^2=v_{0H}^2+2(-g)\Delta S\\[5pt]
v^2=0^2-2g(0-H)\\[5pt]
v^2=0-2g(-H)\\[5pt]
v^2=0+2gH\\[5pt]
v^2=\cancel{2g}\left(\frac{v_0^2+2gh}{\cancel{2g}}\right)\\[5pt]
v=\sqrt{v_0^2+2gh} \tag{IV}
\end{gather}
\]
- Sphère C:
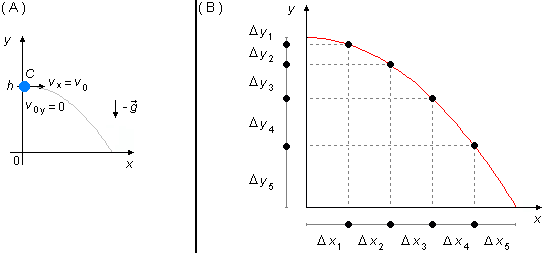
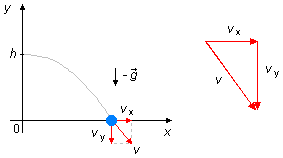
Dans la direction x, il n'y a pas d'accélération agissant sur la sphère, elle est en Mouvement Uniforme (MU), pour un même intervalle de temps, les déplacements le long de l'axe x sont égaux (Δ x1=Δ x2=Δ x3=Δ x4=Δ x5 - Figure 3-B). La composante de la vitesse dans cette direction sera la propre vitesse de lancement de la sphère v0
\[
\begin{gather}
v_x=v_0 \tag{V}
\end{gather}
\]
Dans la direction y, nous avons l'accélération de la presanteur agissant sur la sphère, donc elle est
en Mouvement Uniformément Varié (MUV), pour un même intervalle de temps, les déplacements sont
de plus en plus grands (Δ y1<Δ y2<Δ
y3<Δ y4<Δ y5). Initialement, la
vitesse est nulle v0y = 0, la vitesse dans cette direction est donnée par l'équation (I),
avec a = −g
\[
\begin{gather}
v_y^2=v_{0y}^2+2(-g)\Delta S_y\\[5pt]
v_y^2=0^2-2g(0-h)\\[5pt]
v_y^2=0-2g(-h)\\[5pt]
v_y^2=2gh \tag{VI}
\end{gather}
\]
La vitesse avec laquelle la sphère atteint le sol est donnée par la somme des composantes dans les
directions x et y, données par les équations (V) et (VI) respectivement, en utilisant le
Théorème de Pythagore (Figure 4)
\[
\begin{gather}
v^2=v_x^2+v_y^2\\[5pt]
v^2=v_0^2+2gh\\[5pt]
v=\sqrt{v_0^2+2gh} \tag{VII}
\end{gather}
\]
En comparant les équations (II), (IV) et (VII), nous voyons que toutes les sphères atteignent le sol avec la même vitesse.
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .