Ejercicio Resuelto sobre Movimiento Bidimensional
publicidad
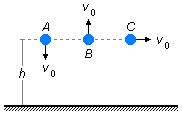
Tres esferas idénticas se lanzan desde una misma altura h con velocidades de igual magnitud. La
esfera A se lanza verticalmente hacia abajo, la B se lanza verticalmente hacia arriba y la
C se lanza horizontalmente. ¿Cuál de ellas llega al suelo con la mayor velocidad en módulo,
despreciando la resistencia del aire?
Datos del problema:
- Velocidad de lanzamiento: v0;
- Altura del punto de lanzamiento: h.
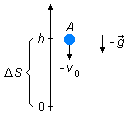
- Esfera A:
\[
\begin {gather}
\bbox[#99CCFF,10px]
{v^2=v_0^2+2a\Delta S} \tag{I}
\end{gather}
\]
\[
\begin{gather}
v^2=(-v_0)^2+2(-g)\Delta S\\[5pt]
v^2=v_0^2-2g(0-h)\\[5pt]
v^2=v_0^2-2g(-h)\\[5pt]
v^2=v_0^2+2gh\\[5pt]
v=\sqrt{v_0^2+2gh} \tag{II}
\end{gather}
\]
- Esfera B:
En la primera parte la velocidad inicial de lanzamiento es positiva, está orientada en el mismo sentido del referencial, y la velocidad final es nula, vH = 0, es el instante en que la esfera se detiene e invierte el movimiento para comenzar a caer (Figura 2-A).
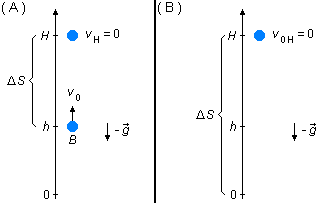
Escribiendo la ecuación (I) para la primera parte encontramos la altura alcanzada por la esfera
\[
\begin{gather}
v^2=v_0^2+2a\Delta S\\[5pt]
v_H^2=v_0^2+2(-g)\Delta S\\[5pt]
0^2=v_0^2-2g(H-h)\\[5pt]
0=v_0^2-2gH+2gh\\[5pt]
2gH=v_0^2+2gh\\[5pt]
H=\frac{v_0^2+2gh}{2g} \tag{III}
\end{gather}
\]
En la segunda parte, caída libre, la velocidad inicial será la velocidad final de la primera parte, que será
nula, v0H = vH = 0, y la altura inicial será dada por la ecuación
(III). Aplicando la ecuación (I) tenemos la velocidad con que la esfera llega al suelo
\[
\begin{gather}
v^2=v_0^2+2a\Delta S\\[5pt]
v^2=v_{0H}^2+2(-g)\Delta S\\[5pt]
v^2=0^2-2g(0-H)\\[5pt]
v^2=0-2g(-H)\\[5pt]
v^2=0+2gH\\[5pt]
v^2=\cancel{2g}\left(\frac{v_0^2+2gh}{\cancel{2g}}\right)\\[5pt]
v=\sqrt{v_0^2+2gh} \tag{IV}
\end{gather}
\]
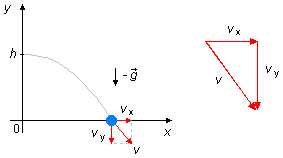
- Esfera C:
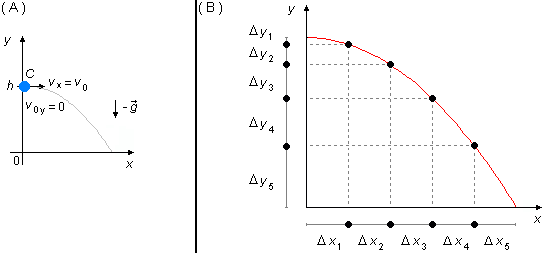
En la dirección x no hay aceleración actuando sobre la esfera, está en Movimiento Uniforme (MU), para un mismo intervalo de tiempo los desplazamientos a lo largo del eje x son iguales (Δ x1=Δ x2=Δ x3=Δ x4=Δ x5 - Figura 3-B). El componente de la velocidad en esta dirección será la propia velocidad de lanzamiento de la esfera v0
\[
\begin{gather}
v_x=v_0 \tag{V}
\end{gather}
\]
En la dirección y tenemos la aceleración de la gravedad actuando sobre la esfera, por lo tanto, está
en Movimiento Uniformemente Variado (MUV), para un mismo intervalo de tiempo los
desplazamientos son cada vez mayores (Δ y1<Δ y2<Δ
y3<Δ y4<Δ y5). Inicialmente la
velocidad es nula v0y = 0, la velocidad en esta dirección está dada por la ecuación (I),
con a = −g
\[
\begin{gather}
v_y^2=v_{0y}^2+2(-g)\Delta S_y\\[5pt]
v_y^2=0^2-2g(0-h)\\[5pt]
v_y^2=0-2g(-h)\\[5pt]
v_y^2=2gh \tag{VI}
\end{gather}
\]
La velocidad con que la esfera alcanza el suelo está dada por la suma de los componentes en las
direcciones x y y, dadas por las ecuaciones (V) y (VI) respectivamente, usando el
Teorema de Pitágoras (Figura 4).
\[
\begin{gather}
v^2=v_x^2+v_y^2\\[5pt]
v^2=v_0^2+2gh\\[5pt]
v=\sqrt{v_0^2+2gh} \tag{VII}
\end{gather}
\]
Comparando las ecuaciones (II), (IV) y (VII) vemos que todas las esferas llegan al suelo con la misma velocidad.
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .