Exercice Résolu sur les Mouvement Unidimensionnel
publicité   



Deux bateaux partent du même point et se déplacent sur une même ligne droite, avec des vitesses constantes de 25 km/h et 35 km/h. La communication entre les deux bateaux est possible, par radio, tant que la distance entre eux ne dépasse pas 600 km. Déterminer le temps pendant lequel les deux bateaux peuvent communiquer, en supposant que:
a) Les deux bateaux se déplacent dans le même sens;
b) Le bateau le plus lent part deux heures avant l'autre et se déplace dans le même sens;
c) Les deux bateaux partent en même temps et se déplacent dans des sens opposés.


Données du problème:
  • Vitesse du bateau 1:    v1 = 25 km/h;
  • Vitesse du bateau 2:    v2 = 35 km/h;
  • Distance maximale de communication:    Δt = 600 km.
Schéma du problème:

Nous choisissons un référentiel avec l'axe positif orienté vers la droite (Figure 1).

Figure 1

En considérant que le point d'où partent les bateaux est l'origine de le référentiel S01 = S02 = 0

Solution

a) Les bateaux se déplacent à des vitesses constantes, ils sont en Mouvement Rectiligne Uniforme, donné par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \end{gather} \]
en ecrivant cette équation pour chacun des bateaux
\[ \begin{gather} S_1=S_{01}+v_1 t\\[5pt] S_1=0+25t\\[5pt] S_1=25t \tag{I-a} \end{gather} \]
\[ \begin{gather} S_2=S_{02}+v_2 t\\[5pt] S_2=0+35t\\[5pt] S_2=35t \tag{I-b} \end{gather} \]
Le bateau 2, avec la vitesse la plus élevée, s'éloigne du bateau 1 jusqu'à ce que la distance entre les deux soit supérieure à 600 km et que la communication ne soit plus possible (Figure 2).

Figure 2

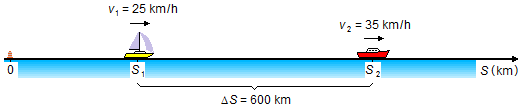
En calculant la différence entre les équations (I-a) et (I-b)
\[ \begin{gather} \frac{ \begin{align} \qquad\quad S_2 &=35t\\ \mathrm{(-)}\qquad S_1 &=25t \end{align} } {S_2-S_1=35t-25t} \end{gather} \]
Étant donné que ΔS = S2 − S1 = 600 km
\[ \begin{gather} \Delta S=10t\\[5pt] 10t=600\\[5pt] t=\frac{600}{10} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t=60\;\mathrm h} \end{gather} \]

b) Le bateau 1 part de l'origine (S01 = 0) et navigue pendant 2 heures jusqu'à atteindre une position S1 sur la trajectoire (Figure 3).

Figure 3

En écrivant l'équation de mouvement pour cette première partie du mouvement
\[ \begin{gather} S_1=S_{01}+v_1 t\\[5pt] S_1=0+25t\\[5pt] S_1=25t \end{gather} \]
après deux heures (t = 2 h), le bateau sera à la position
\[ \begin{gather} S_1=25\times 2\\[5pt] S_1=50\;\mathrm{km} \end{gather} \]
À ce moment, le bateau 2 part de l'origine (S02 = 0) et la position du bateau 1 trouvée ci-dessus devient la position initiale pour la deuxième partie du mouvement (S01 = 50 - Figura 4)

Figure 4

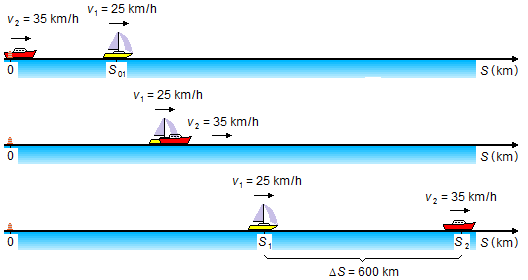
Le bateau 2 dépasse le bateau 1 et s'éloigne jusqu'à ce que la communication entre eux soit impossible, donc les équations de mouvement des bateaux seront
\[ \begin{gather} S_1=S_{01}+v_1 t\\[5pt] S_1=50+25t \tag{II-a} \end{gather} \]
\[ \begin{gather} S_2=S_{02}+v_2 t\\[5pt] S_2=0+35t\\[5pt] S_2=35t \tag{II-b} \end{gather} \]
Calculant la différence entre les deux expressions (II-a) et (II-b)
\[ \begin{gather} \frac{ \begin{align} S_2=35t\\ (\mathrm -)\qquad S_1=50+25t \end{align} } {S_2-S_1=35t-50-25t}\\[5pt] \Delta S=35t-50-25t\\[5pt] 10t=600+50\\[5pt] t=\frac{650}{10} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t=65\;\mathrm h} \end{gather} \]

c) Supposons que le bateau 1 parte dans le sens contraire à la direction de la trajectoire, sa vitesse sera négative (v1=−25 km/h - Figure 4).

Figura 4

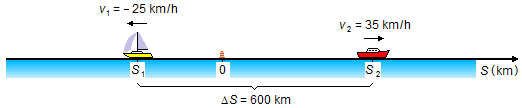
Les équations de ce mouvement pour les deux bateaux seront
\[ \begin{gather} S_1=S_{01}+v_1 t\\[5pt] S_1=0-25t\\[5pt] S_1=-25t \tag{III-a} \end{gather} \]
\[ \begin{gather} S_2=S_{02}+v_2 t\\[5pt] S_2=0+35t \\[5pt] S_2=35t \tag{III-b} \end{gather} \]
En calculant la différence entre les deux équations (III-a) et (III-b)
\[ \begin{gather} \frac{ \begin{align} S_2 &=35t\\ \mathrm{(-)}\qquad S_1 &=-25t \end{align} } {S_2-S_1=35t+25t}\\[5pt] \Delta S=60t\\[5pt] 60t=600\\[5pt] t=\frac{600}{60} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t=10\;\mathrm h} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .