Solved Problem on One-dimensional Motion
advertisement
Two boats depart from the same point and travel on the same straight line, with a constant speed of 25 km/h and 35 km/h. Communication between the two boats is possible by radio as long as the distance between them does not exceed 600 km. Find the time interval during which the two boats can communicate, in the following cases:
a) The two boats move in the same direction;
b) The slower boat departs two hours before the other and moves in the same direction;
c) The two boats depart at the same time and move in opposite directions.
Problem Data:
- Boat 1 speed: v1 = 25 km/h;
- Boat 2 speed: v2 = 35 km/h;
- Maximum communication distance: Δt = 600 km.
We choose a reference frame with the positive axis pointed to the right (Figure 1).

Let us consider that the point from which the boats depart is the origin of the reference frame S01 = S02 = 0
Solution
a) The boats move at constant speeds, the equations of displacement as a function of time is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
writing this equation for the two boats
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=0+\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
S_1=25\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t \tag{I-a}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_2 t\\[5pt]
S_2=0+\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
S_2=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t \tag{I-b}
\end{gather}
\]
The faster boat 2 moves away from boat 1 until the distance between them is greater than 600 km, and
communication is no longer possible (Figure 2).
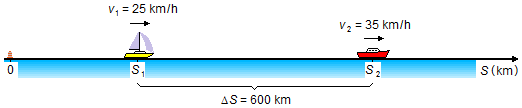
Calculating the difference between the two equations (I-a) and (I-b)
\[
\begin{gather}
\frac{
\begin{align}
S_2 &=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t\\
\mathrm{(-)}\qquad S_1 &=\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t
\end{align}
}
{S_2-S_1=\left(35\;\mathrm{\frac{km}{h}}\right)t-\left(25\;\mathrm{\frac{km}{h}}\right)t}
\end{gather}
\]
We have ΔS = S2 − S1 = 600 km
\[
\begin{gather}
\Delta S=\left(10\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
\left(10\;\mathrm{\small{\frac{km}{h}}}\right)t=600\;\mathrm{km}\\[5pt]
t=\frac{600\;\mathrm{\cancel{km}}}{10\;\mathrm{\frac{\cancel{km}}{h}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=60\;\mathrm h}
\end{gather}
\]
b) Boat 1 departs from the origin (S1=0) and sails for 2 h until it reaches a position S1 on its trajectory (Figure 3).

Writing the equation of motion for this first part of the motion
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=0+\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
S_1=25\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t
\end{gather}
\]
after two hours (t=2h), the boat will be in position
\[
\begin{gather}
S_1=\left(25\;\mathrm{\small{\frac{km}{\cancel h}}}\right)(2\;\mathrm{\cancel h})\\[5pt]
S_1=50\;\mathrm{km}
\end{gather}
\]
At this moment, boat 2 starts from the origin (S02=0), and the position of boat 1, found
above, becomes the starting position for the second part of the movement
(S01=50km - Figure 4).
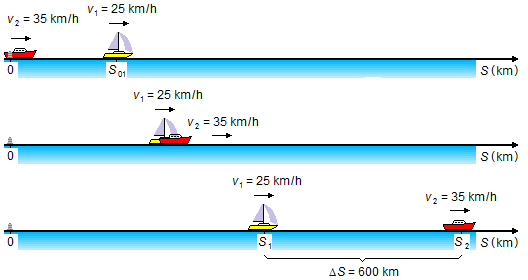
Boat 2 overtakes boat 1 and moves away until communication between them is impossible, so the equations of motion will be
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=50\;\mathrm{km}+\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t \tag{II-a}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_2 t\\[5pt]
S_2=0+\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
S_2=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t \tag{II-b}
\end{gather}
\]
Calculating the difference between the two equations (II-a) and (II-b)
\[
\begin{gather}
\frac{
\begin{align}
S_2=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t\\
(\mathrm -)\qquad S_1=50\;\mathrm{km}+\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t
\end{align}
}
{S_2-S_1=\left(35\;\mathrm{\frac{km}{h}}\right)t-50\;\mathrm{km}-\left(25\;\mathrm{\frac{km}{h} }\right)t}\\[5pt]
\Delta S=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t-50\;\mathrm{km}-\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
\left(10\;\mathrm{\small{\frac{km}{h}}}\right)t=600\;\mathrm{km}+50\;\mathrm{km}\\[5pt]
t=\frac{650\;\mathrm{km}}{10\;\mathrm{\frac{km}{h}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=65\;\mathrm h}
\end{gather}
\]
c) Let us assume that boat 1 departs in the opposite direction to the frame orientation. Thus its velocity will be negative (v1=−25 km/h - Figure 4).
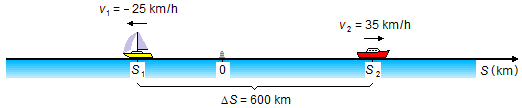
The equations for both boats will be
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=0-\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
S_1=-\left(25\;\mathrm{\small{\frac{km}{h}}}\right)t \tag{III-a}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_2 t\\[5pt]
S_2=0+\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
S_2=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t \tag{III-b}
\end{gather}
\]
Calculating the difference between the two equations (III-a) and (III-b)
\[
\begin{gather}
\frac{
\begin{align}
S_2 &=\left(35\;\mathrm{\frac{km}{h}}\right)t\\
\mathrm{(-)}\qquad S_1 &=\left(-25\;\mathrm{\frac{km}{h}}\right)t
\end{align}
}
{S_2-S_1=\left(35\;\mathrm{\small{\frac{km}{h}}}\right)t+\left(25\;\mathrm{\small{\frac{km}{h}}}\right)}\\[5pt]
\Delta S=\left(60\;\mathrm{\small{\frac{km}{h}}}\right)t\\[5pt]
\left(60\;\mathrm{\small{\frac{km}{h}}}\right)t=600\;\mathrm{km}\\[5pt]
t=\frac{600\;\mathrm{\cancel{km}}}{60\;\mathrm{\frac{\cancel{km}}{h}}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=10\;\mathrm h}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .