Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
Dos barcos parten de un mismo punto y se desplazan sobre una misma recta, con velocidades constantes de 25 km/h y 35 km/h. La comunicación entre los dos barcos es posible, por radio, mientras la distancia entre ellos no supere los 600 km. Determinar el tiempo durante el cual los dos barcos pueden comunicarse, admitiendo que:
a) Los dos barcos se mueven en el mismo sentido;
b) El barco más lento parte dos horas antes que el otro y se mueve en el mismo sentido;
c) Los dos barcos parten al mismo tiempo y se mueven en sentidos opuestos.
Datos del problema:
- Velocidad del barco 1: v1 = 25 km/h;
- Velocidad del barco 2: v2 = 35 km/h;
- Distancia máxima de comunicación: Δt = 600 km.
Tomaamos un sistema de referencia con el eje positivo orientado hacia la derecha (Figura 1).

Considerando que el punto desde donde parten los barcos es el origen del referencial S01 = S02 = 0
Solución
a) Los barcos se mueven con velocidades constantes, están en Movimiento Rectilíneo Uniforme (MRU), dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
escribiendo esta ecuación para cada uno de los barcos
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=0+25t\\[5pt]
S_1=25t \tag{I-a}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_2 t\\[5pt]
S_2=0+35t\\[5pt]
S_2=35t \tag{I-b}
\end{gather}
\]
El barco 2, de mayor velocidad, se aleja del barco 1 hasta que la distancia entre los dos sea mayor que
600 km y la comunicación deje de ser posible (Figura 2).
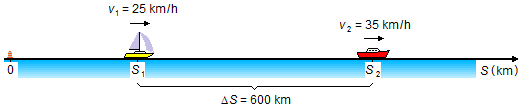
Calculando la diferencia entre las ecuaciones (I-a) y (I-b)
\[
\begin{gather}
\frac{
\begin{align}
\qquad\quad S_2 &=35t\\
\mathrm{(-)}\qquad S_1 &=25t
\end{align}
}
{S_2-S_1=35t-25t}
\end{gather}
\]
Siendo ΔS = S2 − S1 = 600 km
\[
\begin{gather}
\Delta S=10t\\[5pt]
10t=600\\[5pt]
t=\frac{600}{10}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=60\;\mathrm h}
\end{gather}
\]
b) El barco 1 parte desde el origen (S01 = 0) y navega durante 2 horas hasta alcanzar una posición S1 en la trayectoria (Figura 3).

Escribiendo la ecuación de movimiento para esta primera parte del movimiento
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=0+25t\\[5pt]
S_1=25t
\end{gather}
\]
después de dos horas (t = 2 h), el barco estará en la posición
\[
\begin{gather}
S_1=25\times 2\\[5pt]
S_1=50\;\mathrm{km}
\end{gather}
\]
En este instante, el barco 2 parte desde el origen (S02 = 0) y la posición del barco 1
encontrada arriba pasa a ser la posición inicial para la segunda parte del movimiento
(S01 = 50 - Figura 4)
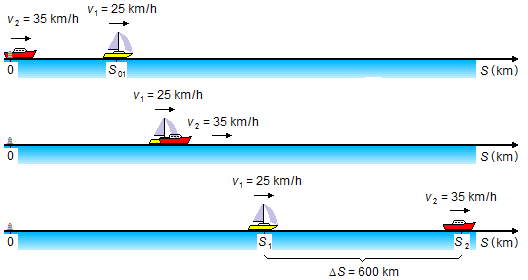
El barco 2 sobrepasa al barco 1 y se aleja hasta que la comunicación entre ellos sea imposible, así que las ecuaciones de movimiento de los barcos serán
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=50+25t \tag{II-a}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_2 t\\[5pt]
S_2=0+35t\\[5pt]
S_2=35t \tag{II-b}
\end{gather}
\]
Calculando la diferencia entre las dos expresiones (II-a) y (II-b)
\[
\begin{gather}
\frac{
\begin{align}
S_2=35t\\
(\mathrm -)\qquad S_1=50+25t
\end{align}
}
{S_2-S_1=35t-50-25t}\\[5pt]
\Delta S=35t-50-25t\\[5pt]
10t=600+50\\[5pt]
t=\frac{650}{10}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=65\;\mathrm h}
\end{gather}
\]
c) Vamos a adoptar que el barco 1 parte en sentido contrario a la orientación de la trayectoria, su velocidad será negativa (v1=−25 km/h - Figura 4).
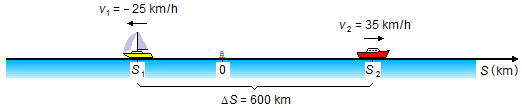
Las ecuaciones de este movimiento para los dos barcos serán
\[
\begin{gather}
S_1=S_{01}+v_1 t\\[5pt]
S_1=0-25t\\[5pt]
S_1=-25t \tag{III-a}
\end{gather}
\]
\[
\begin{gather}
S_2=S_{02}+v_2 t\\[5pt]
S_2=0+35t \\[5pt]
S_2=35t \tag{III-b}
\end{gather}
\]
Calculando la diferencia entre las dos ecuaciones (III-a) y (III-b)
\[
\begin{gather}
\frac{
\begin{align}
S_2 &=35t\\
\mathrm{(-)}\qquad S_1 &=-25t
\end{align}
}
{S_2-S_1=35t+25t}\\[5pt]
\Delta S=60t\\[5pt]
60t=600\\[5pt]
t=\frac{600}{60}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t=10\;\mathrm h}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .