Exercice Résolu sur les Mouvement Unidimensionnel
publicité
Le mouvement d'un corps est donné par le graphique de la vitesse en fonction du temps, v = f(t):
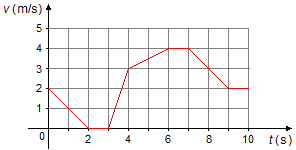
Déterminer:
a) L'espace parcouru entre 1 s et 9 s;
b) La vitesse moyenne entre 1 s et 9 s;
c) L'accélération moyenne entre 1 s et 9 s.
Solution
a) Sur un graphique de la vitesse en fonction du temps, v = f(t), l'espace parcouru est égal à l'aire sous la courbe.
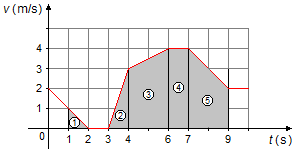
Nous pouvons diviser le graphique en les zones suivantes (Figure 1):
- Entre les instants 1 s et 2 s, un triangle d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{(2-1)\times 1}{2}\\[5pt]
A_1=\frac{1\times 1}{2}\\[5pt]
A_1=\frac{1}{2}\\[5pt]
A_1=0,5
\end{gather}
\]
- Entre les instants 2 s et 3 s, la vitesse est nulle, donc le mobile est resté au repos, il n'y a pas eu de déplacement.
- Entre les instants 3 s et 4 s, un triangle d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4-3)\times 3}{2}\\[5pt]
A_2=\frac{1\times 3}{2}\\[5pt]
A_2=\frac{3}{2}\\[5pt]
A_2=1,5
\end{gather}
\]
- Entre les instants 4 s et 6 s, un trapèze d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(4+3)\times(6-4)}{2}\\[5pt]
A_3=\frac{7\times 2}{2}\\[5pt]
A_3=7
\end{gather}
\]
- Entre les instants 6 s et 7 s, un rectangle d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_4=L_1 L_2}
\end{gather}
\]
\[
\begin{gather}
A_4=4\times (7-6)\\[5pt]
A_4=4\times 1\\[5pt]
A_4=4
\end{gather}
\]
- Entre les instants 7 s et 9 s, un trapèze d'aire égale à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_5=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_5=\frac{(4+2)\times(9-7)}{2}\\[5pt]
A_5=\frac{6\times 2}{2}\\[5pt]
A_5=6
\end{gather}
\]
L'espace parcouru sera l'aire totale donnée par la somme des aires trouvées
\[
\begin{gather}
\Delta S=A_{1}+A_{2}+A_{3}+A_{4}+A_{5}\\[5pt]
\Delta S=0,5+1,5+7+4+6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=19\;\mathrm m}
\end{gather}
\]
b) La vitesse moyenne est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_m=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
en utilisant l'espace parcouru trouvé dans la partie (a)
\[
\begin{gather}
v_m=\frac{19}{9-1}\\[5pt]
v_m=\frac{19}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_m\approx 2,4\;\mathrm{m/s}}
\end{gather}
\]
c) L'accélération moyenne est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_m=\frac{\Delta v}{\Delta t}}
\end{gather}
\]
du graphique, nous savons que pour t1 = 1 s, la vitesse est v1 = 1 m/s,
et pour t2 = 9 s, la vitesse est v2 = 2 m/s
\[
\begin{gather}
a_m=\frac{2-1}{9-1}\\[5pt]
a_m=\frac{1}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_m\approx 0,1\;\mathrm{m/s^2}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .