Exercício Resolvido de Movimento Unidimensional
publicidade
O movimento de um corpo é dado pelo gráfico da velocidade em função do tempo, v = f(t):

Determinar:
a) O espaço percorrido entre 1 s e 9 s;
b) A velocidade média entre 1 s e 9 s;
c) A aceleração média entre 1 s e 9 s.
Solução
a) Em um gráfico da velocidade em função do tempo, v = f(t), o espaço percorrido é igual a área sob a curva.
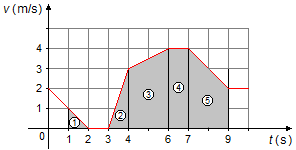
Podemos dividir o gráfico nas seguintes áreas (Figura 1):
- Entre os instantes 1 s e 2 s, um triângulo de área igual à
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{(2-1)\times 1}{2}\\[5pt]
A_1=\frac{1\times 1}{2}\\[5pt]
A_1=\frac{1}{2}\\[5pt]
A_1=0,5
\end{gather}
\]
- Entre os instantes 2 s e 3 s, a velocidade é nula, portanto o móvel permaneceu em repouso, não houve deslocamento.
- Entre os instantes 3 s e 4 s, um triângulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4-3)\times 3}{2}\\[5pt]
A_2=\frac{1\times 3}{2}\\[5pt]
A_2=\frac{3}{2}\\[5pt]
A_2=1,5
\end{gather}
\]
- Entre os instantes 4 s e 6 s, um trapézio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(4+3)\times(6-4)}{2}\\[5pt]
A_3=\frac{7\times 2}{2}\\[5pt]
A_3=7
\end{gather}
\]
- Entre os instantes 6 s e 7 s, um retângulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_4=L_1 L_2}
\end{gather}
\]
\[
\begin{gather}
A_4=4\times (7-6)\\[5pt]
A_4=4\times 1\\[5pt]
A_4=4
\end{gather}
\]
- Entre os instantes 7 s e 9 s, um trapézio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_5=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_5=\frac{(4+2)\times(9-7)}{2}\\[5pt]
A_5=\frac{6\times 2}{2}\\[5pt]
A_5=6
\end{gather}
\]
O espaço percorrido será a área total dada pela soma das áreas encontradas
\[
\begin{gather}
\Delta S=A_{1}+A_{2}+A_{3}+A_{4}+A_{5}\\[5pt]
\Delta S=0,5+1,5+7+4+6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=19\;\mathrm m}
\end{gather}
\]
b) A velocidade média é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_m=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
usando o espaço percorrido encontrado no item (a)
\[
\begin{gather}
v_m=\frac{19}{9-1}\\[5pt]
v_m=\frac{19}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_m\approx 2,4\;\mathrm{m/s}}
\end{gather}
\]
c) A aceleração média é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_m=\frac{\Delta v}{\Delta t}}
\end{gather}
\]
do gráfico temos que para t1 = 1 s a velocidade vale v1 = 1 m/s, e para
t2 = 9 s a velocidade vale v2 = 2 m/s
\[
\begin{gather}
a_m=\frac{2-1}{9-1}\\[5pt]
a_m=\frac{1}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_m\approx 0,1\;\mathrm{m/s^2}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .