Ejercicio Resuelto sobre Movimiento Unidimensional
publicidad
El movimiento de un cuerpo está dado por el gráfico de la velocidad en función del tiempo, v = f(t):
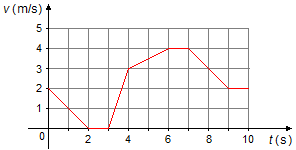
Determinar:
a) El espacio recorrido entre 1 s y 9 s;
b) La velocidad media entre 1 s y 9 s;
c) La aceleración media entre 1 s y 9 s.
Solución
a) En un gráfico de la velocidad en función del tiempo, v = f(t), el espacio recorrido es igual al área bajo la curva.
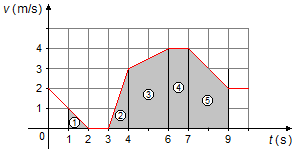
Podemos dividir el gráfico en las siguientes áreas (Figura 1):
- Entre los instantes 1 s y 2 s, un triángulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{(2-1)\times 1}{2}\\[5pt]
A_1=\frac{1\times 1}{2}\\[5pt]
A_1=\frac{1}{2}\\[5pt]
A_1=0,5
\end{gather}
\]
- Entre los instantes 2 s y 3 s, la velocidad es nula, por lo tanto, el móvil permanece en reposo, no hay desplazamiento.
- Entre los instantes 3 s y 4 s, un triángulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4-3)\times 3}{2}\\[5pt]
A_2=\frac{1\times 3}{2}\\[5pt]
A_2=\frac{3}{2}\\[5pt]
A_2=1,5
\end{gather}
\]
- Entre los instantes 4 s y 6 s, un trapecio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(4+3)\times(6-4)}{2}\\[5pt]
A_3=\frac{7\times 2}{2}\\[5pt]
A_3=7
\end{gather}
\]
- Entre los instantes 6 s y 7 s, un rectángulo de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_4=L_1 L_2}
\end{gather}
\]
\[
\begin{gather}
A_4=4\times (7-6)\\[5pt]
A_4=4\times 1\\[5pt]
A_4=4
\end{gather}
\]
- Entre los instantes 7 s y 9 s, un trapecio de área igual a
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_5=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_5=\frac{(4+2)\times(9-7)}{2}\\[5pt]
A_5=\frac{6\times 2}{2}\\[5pt]
A_5=6
\end{gather}
\]
El espacio recorrido será el área total dada por la suma de las áreas encontradas
\[
\begin{gather}
\Delta S=A_{1}+A_{2}+A_{3}+A_{4}+A_{5}\\[5pt]
\Delta S=0,5+1,5+7+4+6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=19\;\mathrm m}
\end{gather}
\]
b) La velocidad media se calcula mediante
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_m=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
utilizando el espacio recorrido encontrado en el apartado (a)
\[
\begin{gather}
v_m=\frac{19}{9-1}\\[5pt]
v_m=\frac{19}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_m\approx 2,4\;\mathrm{m/s}}
\end{gather}
\]
c) La aceleración media se calcula mediante
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_m=\frac{\Delta v}{\Delta t}}
\end{gather}
\]
del gráfico, sabemos que para t1 = 1 s, la velocidad es v1 = 1 m/s, y
para t2 = 9 s, la velocidad es v2 = 2 m/s
\[
\begin{gather}
a_m=\frac{2-1}{9-1}\\[5pt]
a_m=\frac{1}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_m\approx 0,1\;\mathrm{m/s^2}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .