Solved Problem on One-dimensional Motion
advertisement
The velocity-time graph v = f(t) describes the motion of a body:
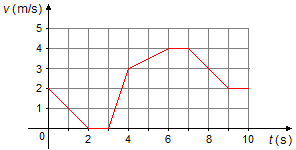
Find:
a) The displacement between 1 s and 9 s;
b) The average speed between 1 s and 9 s;
c) The average acceleration between 1 s and 9 s.
Solution
a) In a velocity-time graph v = f(t), the displacement is equal to the area under the curve
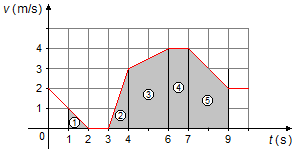
We can divide the graph into the following areas (figure 1)
- Between the instants, 1 s and 2 s, a triangle of area equal to
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_1=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_1=\frac{(2-1)\times 1}{2}\\[5pt]
A_1=\frac{1\times 1}{2}\\[5pt]
A_1=\frac{1}{2}\\[5pt]
A_1=0.5
\end{gather}
\]
- Between the instants, 2 s and 3 s, the speed is zero, the body remained at rest, there was no displacement.
- Between the instants, 3 s and 4 s, a triangle of area equal to
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_2=\frac{Bh}{2}}
\end{gather}
\]
\[
\begin{gather}
A_2=\frac{(4-3)\times 3}{2}\\[5pt]
A_2=\frac{1\times 3}{2}\\[5pt]
A_2=\frac{3}{2}\\[5pt]
A_2=1.5
\end{gather}
\]
- Between the instants, 4 s and 6 s, a trapezoid of area equal to
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_3=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_3=\frac{(4+3)\times(6-4)}{2}\\[5pt]
A_3=\frac{7\times 2}{2}\\[5pt]
A_3=7
\end{gather}
\]
- Between the instants, 6 s and 7 s, a rectangle of area equal to
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_4=L_1 L_2}
\end{gather}
\]
\[
\begin{gather}
A_4=4\times (7-6)\\[5pt]
A_4=4\times 1\\[5pt]
A_4=4
\end{gather}
\]
- Between the instants, 7 s and 9 s, a trapezoid of area equal to
\[
\begin{gather}
\bbox[#99CCFF,10px]
{A_5=\frac{(B+b)h}{2}}
\end{gather}
\]
\[
\begin{gather}
A_5=\frac{(4+2)\times(9-7)}{2}\\[5pt]
A_5=\frac{6\times 2}{2}\\[5pt]
A_5=6
\end{gather}
\]
The total area will be the sum of the areas found above
\[
\begin{gather}
\Delta S=A_{1}+A_{2}+A_{3}+A_{4}+A_{5}\\[5pt]
\Delta S=0.5+1.5+7+4+6
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=19\;\mathrm m}
\end{gather}
\]
b) The average speed is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v_m=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
using the displacement in item (a)
\[
\begin{gather}
\bar v=\frac{19}{9-1}\\[5pt]
\bar v=\frac{19}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\bar v\approx 2.4\;\mathrm{m/s}}
\end{gather}
\]
c) The average acceleration is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\bar a=\frac{\Delta v}{\Delta t}}
\end{gather}
\]
From the graph, we have for t1 = 1 s the speed is v1 = 1 m/s , and for
t2 = 9 s the velocity is v2 = 2 m/s
\[
\begin{gather}
\bar a=\frac{2-1}{9-1}\\[5pt]
\bar a=\frac{1}{8}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\bar a\approx 0,1\;\mathrm{m/s^2}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .