Exercice Résolu sur les Mouvement Circulaire
publicité
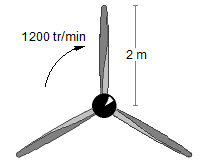
Une hélice d'avion a des pales de 2 m de longueur et tourne à une fréquence de 1200 tr/min. Calculer:
a) La fréquence en hertz;
b) La période des rotations;
c) La vitesse angulaire de l'hélice;
d) La vitesse linéaire d'un point situé à l'extrémité d'une des pales de l'hélice;
e) Le module de l'accélération centripète.
a) La fréquence en hertz;
b) La période des rotations;
c) La vitesse angulaire de l'hélice;
d) La vitesse linéaire d'un point situé à l'extrémité d'une des pales de l'hélice;
e) Le module de l'accélération centripète.
Données du problème:
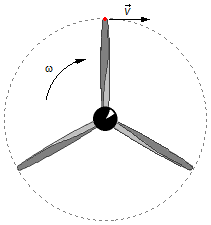
En prenant un point à l'extrémité de l'hélice, la vitesse, \( \vec{v} \) , sera tangente à la trajectoire et l'hélice tourne avec une vitesse angulaire ω (Figure 1).
- Longueur de l'hélice (rayon de la circonférence): r = 2 m;
- Fréquence de rotation: f = 1200 rpm.
En prenant un point à l'extrémité de l'hélice, la vitesse, \( \vec{v} \) , sera tangente à la trajectoire et l'hélice tourne avec une vitesse angulaire ω (Figure 1).
Solution
a) Convertir la fréquence donnée en tr/min en hertz
\[
\begin{gather}
f=1200\frac{\text{rotations}}{1\;\mathrm{\cancel{min}}}\times\frac{1\;\mathrm{\cancel{min}}}{60\;\mathrm{s}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f=20\;\mathrm{Hz}}
\end{gather}
\]
Remarque: les rotations sont un nombre adimensionnel, donc elles n'apparaissent pas
dans le résultat final.
b) La période en fonction de la fréquence sera donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{T=\frac{1}{f}}
\end{gather}
\]
\[
\begin{gather}
T=\frac{1}{20}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=0,05\;\mathrm s}
\end{gather}
\]
c) La vitesse angulaire en fonction de la fréquence sera donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega =2\pi f}
\end{gather}
\]
en utilisant la fréquence obtenue dans le point (a)
\[
\begin{gather}
\omega=2\times\pi\times 20
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\omega=40 \pi \;\mathrm{rad/s}}
\end{gather}
\]
Remarque: la vitesse angulaire peut également être obtenue en utilisant la période calculée
dans le point (b), l'expression de la vitesse angulaire en fonction de la période sera
\[
\begin{gather}
\omega=\frac{2\pi}{T}\\[5pt]
\omega=\frac{2\pi}{0,05}=40\pi\;\mathrm{rad/s}
\end{gather}
\]
d) En utilisant la valeur \( \pi=3,14 \) la vitesse linéaire sera
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v =\omega r}
\end{gather}
\]
\[
\begin{gather}
v=40\times 3,14\times 2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v \approx 251\;\mathrm{m/s}}
\end{gather}
\]
e) Le module de l'accélération centripète est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{251^2}{2}\\[5pt]
|\;a_{cp}\;|=\frac{63001}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{|\;a_{cp}\;|\approx 31501\;\mathrm{m/s^2}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .