Ejercicio Resuelto sobre Movimiento Circular
publicidad
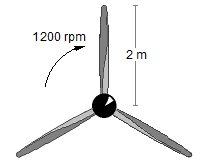
Una hélice de avión tiene palas de 2 m de longitud y giran a una frecuencia de 1200 rpm. Calcula:
a) La frecuencia en hertz;
b) El período de las rotaciones;
c) La velocidad angular de la hélice;
d) La velocidad escalar de un punto situado en la punta de una de las palas de la hélice;
e) El módulo de la aceleración centrípeta.
a) La frecuencia en hertz;
b) El período de las rotaciones;
c) La velocidad angular de la hélice;
d) La velocidad escalar de un punto situado en la punta de una de las palas de la hélice;
e) El módulo de la aceleración centrípeta.
Datos del problema:
Tomando un punto en el extremo de la hélice, la velocidad, \( \vec{v} \) , será tangente a la trayectoria y la hélice gira con una velocidad angular ω (Figura 1).
- Longitud de la hélice (radio de la circunferencia): r = 2 m;
- Frecuencia de rotación: f = 1200 rpm.
Tomando un punto en el extremo de la hélice, la velocidad, \( \vec{v} \) , será tangente a la trayectoria y la hélice gira con una velocidad angular ω (Figura 1).

Solución
a) Convirtiendo la frecuencia dada en rpm a hertz
\[
\begin{gather}
f=1200\frac{\text{rotaciones}}{1\;\mathrm{\cancel{min}}}\times\frac{1\;\mathrm{\cancel{min}}}{60\;\mathrm{s}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f=20\;\mathrm{Hz}}
\end{gather}
\]
Observación: rotaciones son adimensionales, por lo que no aparecen en el resultado
final.
b) El período en función de la frecuencia será dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{T=\frac{1}{f}}
\end{gather}
\]
\[
\begin{gather}
T=\frac{1}{20}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=0,05\;\mathrm s}
\end{gather}
\]
c) La velocidad angular en función de la frecuencia será dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega =2\pi f}
\end{gather}
\]
utilizando la frecuencia obtenida en el ítem (a)
\[
\begin{gather}
\omega=2\times\pi\times 20
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\omega=40 \pi \;\mathrm{rad/s}}
\end{gather}
\]
Observación: la velocidad angular también puede ser obtenida utilizando el período calculado
en el ítem (b), la expresión para la velocidad angular en función del período será
\[
\begin{gather}
\omega=\frac{2\pi}{T}\\[5pt]
\omega=\frac{2\pi}{0,05}=40\pi\;\mathrm{rad/s}
\end{gather}
\]
d) Tomando \( \pi=3,14 \) la velocidad escalar será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v =\omega r}
\end{gather}
\]
\[
\begin{gather}
v=40\times 3,14\times 2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v \approx 251\;\mathrm{m/s}}
\end{gather}
\]
e) El módulo de la aceleración centrípeta es dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{251^2}{2}\\[5pt]
|\;a_{cp}\;|=\frac{63001}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{|\;a_{cp}\;|\approx 31501\;\mathrm{m/s^2}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .