Solved Problem on Circular Motion
DE
ES
FR
PT-BR
advertisement
An airplane propeller has blades 2 m in length and rotates with a frequency of 1200 rpm. Calculate:
a) The frequency in hertz;
b) The period of rotations;
c) The angular speed of the propeller;
d) The speed of a point situated at the tip of one of the propeller blades;
e) The magnitude of the centripetal acceleration.
a) The frequency in hertz;
b) The period of rotations;
c) The angular speed of the propeller;
d) The speed of a point situated at the tip of one of the propeller blades;
e) The magnitude of the centripetal acceleration.
Problem data:
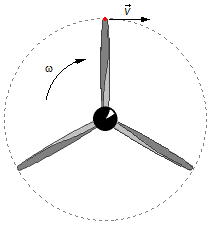
Taking a point at the tip of the propeller, we have the velocity, \( \vec{v} \) , it will be tangent to the trajectory, and the propeller rotates with angular speed ω (Figure 1).
- Length of the propeller (radius of the circle): r = 2 m;
- Frequency of rotation: f = 1200 rpm.
Taking a point at the tip of the propeller, we have the velocity, \( \vec{v} \) , it will be tangent to the trajectory, and the propeller rotates with angular speed ω (Figure 1).
Solution:
a) Converting the frequency given in rpm to hertz
\[
\begin{gather}
f=1200\frac{\text{rotations}}{1\;\mathrm{\cancel{min}}}\times\frac{1\;\mathrm{\cancel{min}}}{60\;\mathrm{s}}
\end{gather}
\]
\[
\begin{gather}
\bbox[background:#FFCCCC; padding:10px; border-radius:10px;]
{f=20\;\mathrm{Hz}}
\end{gather}
\]
Note: rotations is a dimensionless number, which is why it does not appear in
the final result.
b) The period as a function of frequency will be
\[
\begin{gather}
\bbox[background:#99CCFF; padding:10px; border-radius:10px;]
{T=\frac{1}{f}}
\end{gather}
\]
\[
\begin{gather}
T=\frac{1}{20\;\mathrm{Hz}}
\end{gather}
\]
\[
\begin{gather}
\bbox[background:#FFCCCC; padding:10px; border-radius:10px;]
{T=0.05\;\mathrm s}
\end{gather}
\]
c) The angular velocity as a function of frequency is given by
\[
\begin{gather}
\bbox[background:#99CCFF; padding:10px; border-radius:10px;]
{\omega =2\pi f}
\end{gather}
\]
using the frequency given in the problem
\[
\begin{gather}
\omega=2\times\pi\times\left(20\;\mathrm{Hz}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[background:#FFCCCC; padding:10px; border-radius:10px;]
{\omega=40 \pi \;\mathrm{rad/s}}
\end{gather}
\]
Note: we can obtain the angular speed using the period calculated in item (b). The
expression for the angular speed as a function of period will be
\[
\begin{gather}
\omega=\frac{2\pi}{T} \\[5pt]
\omega=\frac{2\pi}{0.05\;\mathrm s}=40\pi\;\mathrm{rad/s}
\end{gather}
\]
d) Letting \( \pi=3.14 \) the speed will be
\[
\begin{gather}
\bbox[background:#99CCFF; padding:10px; border-radius:10px;]
{v =\omega r}
\end{gather}
\]
\[
\begin{gather}
v=\left(40\times 3.14\;\mathrm{\frac{rad}{s}}\right)\times\left(2\;\mathrm m\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[background:#FFCCCC; padding:10px; border-radius:10px;]
{v \approx 251\;\mathrm{m/s}}
\end{gather}
\]
e) The magnitude of centripetal acceleration is given by
\[
\begin{gather}
\bbox[background:#99CCFF; padding:10px; border-radius:10px;]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{\left(251\;\mathrm{\frac{m}{s}}\right)^2}{2\;\mathrm m} \\[5pt]
|\;a_{cp}\;|=\frac{63001\;\mathrm{\frac{m^{\cancel 2}}{s^2}}}{2\;\mathrm{\cancel m}}
\end{gather}
\]
\[
\begin{gather}
\bbox[background:#FFCCCC; padding:10px; border-radius:10px;]
{|\;a_{cp}\;|\approx 31501\;\mathrm{m/s^2}}
\end{gather}
\]
advertisement