Exercício Resolvido de Movimento Circular
publicidade
Uma hélice de avião possui pás de 2 m de comprimento e giram com frequência de 1200 rpm. Calcule:
a) A frequência em hertz;
b) O período das rotações;
c) A velocidade angular da hélice;
d) A velocidade escalar de um ponto situado na ponta de uma das pás da hélice;
e) O módulo da aceleração centrípeta.
a) A frequência em hertz;
b) O período das rotações;
c) A velocidade angular da hélice;
d) A velocidade escalar de um ponto situado na ponta de uma das pás da hélice;
e) O módulo da aceleração centrípeta.

Dados do problema:
Tomando-se um ponto na extremidade da hélice temos que a velocidade, \( \vec{v} \) , será tangente à trajetória e a hélice gira com velocidade angular ω (Figura 1).
- Comprimento da hélice (raio da circunferência): r = 2 m;
- Frequência de rotação: f = 1200 rpm.
Tomando-se um ponto na extremidade da hélice temos que a velocidade, \( \vec{v} \) , será tangente à trajetória e a hélice gira com velocidade angular ω (Figura 1).
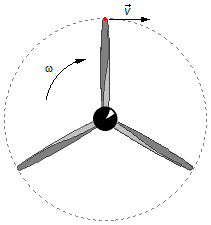
Solução
a) Convertendo a frequência dada em rpm para hertz
\[
\begin{gather}
f=1200\frac{\text{rotações}}{1\;\mathrm{\cancel{min}}}\times\frac{1\;\mathrm{\cancel{min}}}{60\;\mathrm{s}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{f=20\;\mathrm{Hz}}
\end{gather}
\]
Observação: rotações é um número adimensional, por isso não aparece no resultado
final.
b) O período em função da frequência será dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{T=\frac{1}{f}}
\end{gather}
\]
\[
\begin{gather}
T=\frac{1}{20}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T=0,05\;\mathrm s}
\end{gather}
\]
c) A velocidade angular em função da frequência será dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega =2\pi f}
\end{gather}
\]
usando a frequência obtida no item (a)
\[
\begin{gather}
\omega=2\times\pi\times 20
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\omega=40 \pi \;\mathrm{rad/s}}
\end{gather}
\]
Observação: a velocidade angular também pode ser obtida usando o período calculado no item
(b), a expressão para a velocidade angular em função do período será
\[
\begin{gather}
\omega=\frac{2\pi}{T}\\[5pt]
\omega=\frac{2\pi}{0,05}=40\pi\;\mathrm{rad/s}
\end{gather}
\]
d) Adotando \( \pi=3,14 \) a velocidade escalar será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v =\omega r}
\end{gather}
\]
\[
\begin{gather}
v=40\times 3,14\times 2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v \approx 251\;\mathrm{m/s}}
\end{gather}
\]
e) O módulo da aceleração centrípeta é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{251^2}{2}\\[5pt]
|\;a_{cp}\;|=\frac{63001}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{|\;a_{cp}\;|\approx 31501\;\mathrm{m/s^2}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .