Ejercicio Resuelto sobre Dinámica
publicidad
Un cuerpo, de masa igual a 2 kg con velocidad inicial de 10 m/s en sentido positivo, está bajo la acción
de una fuerza variable en función de la posición, dada por
\[
\begin{gather}
F_x=-8x \qquad\qquad\text{unidades (SI)}
\end{gather}
\]
¿Cuál será la distancia recorrida por ese cuerpo hasta que su velocidad sea igual a cero?
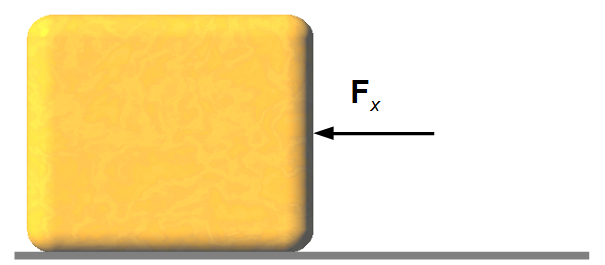
Datos del problema:
- Masa del cuerpo: m = 2 kg;
- Velocidad inicial del cuerpo: v0 = 10.
Tomamos un sistema de referencia con el eje Ox orientado hacia la derecha y el eje Oy hacia arriba (Figura 1).
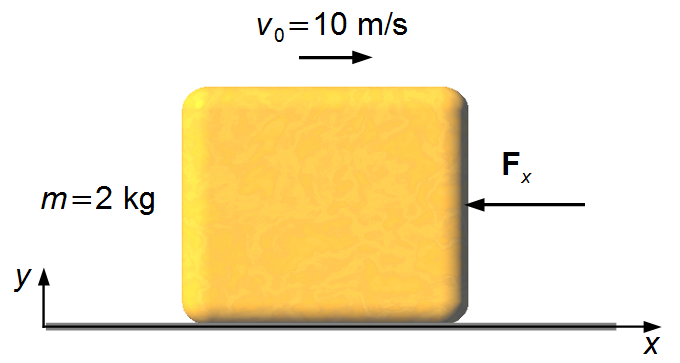
La fuerza dada es negativa, es una fuerza de resistencia que está en la dirección opuesta al movimiento. La fuerza actúa disminuyendo la velocidad del cuerpo hasta que su velocidad final sea igual a cero.
Las Condiciones Iniciales son
\[
\begin{align}
& x(0)=0\\[10pt]
& v_{0}=\frac{dx(0)}{dt}=10\;\mathrm{m/s}
\end{align}
\]
Solución:
Aplicando la Segunda Ley de Newton en la dirección x, la fuerza dada en el problema es la única fuerza en esta dirección
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf F=m\frac{d^2\mathbf x}{dt^2}}
\end{gather}
\]
\[
\begin{gather}
F_x=m\frac{d^2x}{dt^2}\\[5pt]
-8x=2\frac{d^2x}{dt^{2}}\\[5pt]
\frac{d^2x}{dt^2}+4x=0
\end{gather}
\]
Solución de
\( \displaystyle \frac{d^2x}{dt^2}+4x=0 \)
La solución de este tipo de ecuación se encuentra haciendo las sustituciones
La solución de este tipo de ecuación se encuentra haciendo las sustituciones
\[
\begin{align}
& x=\operatorname{e}^{\lambda t}\\[10pt]
& \frac{dx}{dt}=\lambda \operatorname{e}^{\lambda t}\\[10pt]
& \frac{d^2x\theta}{dt^2}=\lambda^2\operatorname{e}^{\lambda t}
\end{align}
\]
sustituyendo en la ecuación diferencial
\[
\begin{gather}
\lambda^2\operatorname{e}^{\lambda t}+4\operatorname{e}^{\lambda t}=0\\[5pt]
\operatorname{e}^{\lambda t}\left(\lambda ^2+4\right)0\\[5pt]
\lambda^2+4=\frac{0}{\operatorname{e}^{\lambda t}}\\[5pt]
\lambda^2+4=0
\end{gather}
\]
esta es la Ecuación Característica cuya solución es
\[
\begin{gather}
\lambda_{1,2}=\pm\sqrt{-4\;}\\[5pt]
\lambda_{1,2}=\pm2\mathrm{i}
\end{gather}
\]
La solución de la ecuación diferencial será
\[
\begin{gather}
x=C_1\operatorname{e}^{\lambda_1 t}+C_2\operatorname{e}^{\lambda_2 t}\\[5pt]
x=C_1\operatorname{e}^{2\mathrm{i}t}+C_{2}\operatorname{e}^{-2\mathrm{i}t}
\end{gather}
\]
donde C1 y C2 son constantes de integración, usando la
Fórmula de Euler
\( \operatorname{e}^{\mathrm{i}\theta}=\cos\theta+\mathrm{i}\operatorname{sen}\theta \)
\[
\begin{gather}
x=C_1\left(\cos2t+\mathrm{i}\operatorname{sen}2t\right)+C_{2}\left(\cos2t-\mathrm{i}\operatorname{sen}2t\right)\\[5pt]
x=C_1\cos2t+\mathrm{i}C_1\operatorname{sen}2t+C_2\cos2t-\mathrm{i}C_2\operatorname{sen}2t\\[5pt]
x=\left(C_1+C_{2}\right)\cos2t+\mathrm{i}\left(C_1-C_{2}\right)\operatorname{sen}2t
\end{gather}
\]
Definiendo dos nuevas constantes α y β en términos de C1 y
C2
\[
\begin{gather}
\alpha\equiv C_1+C_2\\[5pt]
\mathrm{e}\\[5pt]
\beta\equiv\mathrm{i}(C_1-C_2)
\end{gather}
\]
\[
\begin{gather}
x=\alpha\cos 2t+\beta\operatorname{sen}2t \tag{I}
\end{gather}
\]
Derivando la ecuación (I) con respecto al tiempo, la función x(t) es la suma de dos
funciones, la derivada de la suma se obtiene sumando las derivadas
\[
\begin{gather}
(f+g)'=f'+g'
\end{gather}
\]
y las funciones seno y coseno son funciones compuestas, aplicando la Regla de la Cadena
\[
\begin{gather}
\frac{df[w(t)]}{dt}=\frac{df}{dw}\frac{dw}{dt}
\end{gather}
\]
con
\( f=\alpha\cos w \),
\( g=\beta\operatorname{sen}w \)
y
\( w=2t \)
\[
\begin{gather}
\frac{dx}{dt}=\frac{df}{dt}+\frac{dg}{dt} \tag{II}\\[5pt]
\frac{dx}{dt}=\frac{df}{dw}\frac{dw}{dt}+\frac{dg}{dw}\frac{dw}{dt}\\[5pt]
\frac{dx}{dt}=\frac{d\left(\alpha\cos w\right)}{dw}\frac{d\left(2t\right)}{dt}+\frac{d\left(\beta\operatorname{sen}w\right)}{dw}\frac{d\left(2t\right)}{dt}\\[5pt]
\frac{dx}{dt}=\left(-\alpha\operatorname{sen}w\right)(2)+\left(\beta\cos w\right)(2)\\[5pt]
\frac{dx}{dt}=-2ialpha\operatorname{sen}2t+2ibeta\cos2t\\[5pt]
\frac{dx}{dt}=2\left(-\alpha\operatorname{sen}2t+\beta\cos2t\right) \tag{III}
\end{gather}
\]
Sustituyendo las Condiciones Iniciales en las ecuaciones (I) y (III)
\[
\begin{gather}
x(0)=0=\alpha\cos 2\times0+\beta\operatorname{sen}2\times 0\\[5pt]
\alpha=0 \tag{IV}
\end{gather}
\]
\[
\begin{gather}
\frac{dx(0)}{dt}=10=2\left(-0\times\operatorname{sen}2\times 0+\beta\cos 2\times0\right)\\[5pt]
10=2\beta\\[5pt]
\beta=5 \tag{V}
\end{gather}
\]
sustituyendo las constantes (IV) y (V) en la ecuación (I)
\[
\begin{gather}
x=0\cos 2t+5\operatorname{sen}2t
\end{gather}
\]
La ecuación de movimiento está dada por
\[
\begin{gather}
x(t)=5\operatorname{sen}2t \tag{VI}
\end{gather}
\]
Para encontrar el intervalo de tiempo en el cual la velocidad del cuerpo es igual a cero, derivamos la
ecuación (VI)
Derivada de
\( \displaystyle x(t)=5\operatorname{sen}2t \)
La función x(t) es una función compuesta, usando la Regla de la Cadena dada en (II), y haciendo \( f=5\operatorname{sen}w \) y \( w=2t \)
La función x(t) es una función compuesta, usando la Regla de la Cadena dada en (II), y haciendo \( f=5\operatorname{sen}w \) y \( w=2t \)
\[
\begin{gather}
\frac{dx}{dt}=\frac{df}{dw}\frac{dw}{dt}\\[5pt]v(t)=\frac{d\left(5\operatorname{sen}w\right)}{dw}\frac{d\left(2t\right)}{dt}\\[5pt]
v(t)=\left(5\cos w\right)(2)\\[5pt]
v(t)=2\times 5\cos 2t\\[5pt]
v(t)=10\cos 2t
\end{gather}
\]
La ecuación de la velocidad está dada por
\[
\begin{gather}
v(t)=10\cos 2t
\end{gather}
\]
haciendo v(t) = 0
\[
\begin{gather}
0=10\cos 2t\\[5pt]
\cos 2t=0\\[5pt]
2t=\arccos0\\[5pt]
t=\frac{1}{2}\;\arccos 0
\end{gather}
\]
Valores cuyo arcoseno es cero (arccos 0)
\[
\begin{gather}
\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},...,\frac{(2n+1)\pi}{2},...\qquad\qquad n=0,1,2,3,...
\end{gather}
\]
Usando el primer valor para el cual el arcoseno es cero \( \left(\frac{\pi}{2}\right) \), el intervalo de tiempo en el que la velocidad se anula será
\[
\begin{gather}
t=\frac{1}{2}\times{\frac{\pi}{2}}\\[5pt]
t=\frac{\pi}{4}\;\mathrm s
\end{gather}
\]
sustituyendo este valor en la ecuación (VI), la distancia recorrida por el cuerpo hasta detenerse será
\[
\begin{gather}
x\left(\frac{\pi}{4}\right)=5\operatorname{sen}2\times{\frac{\pi}{4}}\\[5pt]
x\left(\frac{\pi}{4}\right)=5\operatorname{sen}\frac{\pi }{2}
\end{gather}
\]
De la Trigonometría
\( \displaystyle \operatorname{sen}\frac{\pi}{2}=1 \)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x=5\;\mathrm m}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .