Exercice Résolu sur les Dynamique
publicité
Un corps, de masse égale à 2 kg avec une vitesse initiale de 10 m/s dans le sens positif, est soumis à
l'action d'une force variable en fonction de la position, donnée par
\[
\begin{gather}
F_x=-8x \qquad\qquad\text{unités (SI)}
\end{gather}
\]
Quelle sera la distance parcourue par ce corps jusqu'à ce que sa vitesse soit nulle?
Données du problème:
- Masse du corps: m = 2 kg;
- Vitesse initiale du corps: v0 = 10.
Nous choisissons un référentiel avec l'axe Ox orienté vers la droite et l'axe Oy vers le haut (Figure 1).
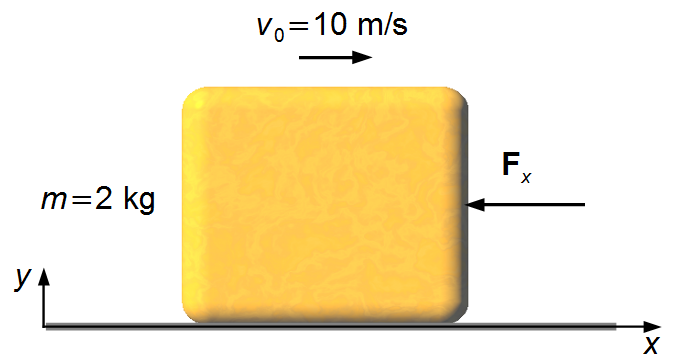
La force donnée est négative, c'est une force de résistance qui est dirigée dans le sens opposé au mouvement. La force agit en diminuant la vitesse du corps jusqu'à ce que sa vitesse finale soit nulle.
Solution:
En appliquant la Deuxième Loi de Newton dans la direction x, la force donnée dans le problème est la seule force dans cette direction
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf F=m\frac{d\mathbf v}{dt}}
\end{gather}
\]
\[
\begin{gather}
F_x=m\frac{dv_x}{dt}\\[5pt]
-8x=2\frac{dv_x}{dt}
\end{gather}
\]
en multipliant et en divisant le côté droit de l'équation par dx
\[
\begin{gather}
-4x=\frac{dv_x}{dt}\frac{dx}{dx}
\end{gather}
\]
en inversant l'ordre des termes d'intégration au dénominateur
\[
\begin{gather}
-4x=\frac{dv_x}{dx}\frac{dx}{dt}
\end{gather}
\]
en appliquant la définition de la vitesse
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{dx}{dt}}
\end{gather}
\]
en intégrant par rapport à dx des deux côtés de l'égalité
\[
\begin{gather}
\int -4x\;dx=\int v_x\frac{dv_x}{dx}\;dx\\[5pt]
\int-4x\;dx=\int v_x\;dv_x
\end{gather}
\]
le facteur constant (−4) sort de l'intégrale du côté gauche
\[
\begin{gather}
-4\int x\;dx=\int v_x\;dv_x
\end{gather}
\]
Intégrale de
\( \displaystyle \int x\;dx \)
\[
\begin{gather}
\int x\;dx=\frac{x^{1+1}}{1+1}+C_1=\frac{x^2}{2}+C_1
\end{gather}
\]
Intégrale de
\( \displaystyle \int v_x\;dv_x \)
\[
\begin{gather}
\int v_x\;dv_x=\frac{v_x^{1+1}}{1+1}+C_2=\frac{v_x^2}{2}+C_2
\end{gather}
\]
où C1 et C2 sont des constantes d'intégration.
\[
\begin{gather}
-4\left(\frac{x^2}{2}+C_1\right)=\frac{v_x^2}{2}+C_2\\[5pt]
-{\frac{4x^2}{2}}-4C_1=\frac{v_x^2}{2}+C_2\\[5pt]
-{\frac{4x^2}{2}}-4C_1-C_2=\frac{v_x^2}{2}
\end{gather}
\]
en définissant les constantes C1 et C2 comme une nouvelle constante
C
\[
\begin{gather}
C\equiv -4C_1-C_2
\end{gather}
\]
L'équation de la vitesse en fonction de la position sera de la forme
\[
\begin{gather}
\frac{v_x^2}{2}=-{\frac{4x^2}{2}}+C
\end{gather}
\]
La constante C est déterminée en utilisant la condition initiale donnée dans le problème, pour
x = 0, et vx = 10 m/s
\[
\begin{gather}
\frac{10^2}{2}=-{\frac{4\times 0^2}{2}}+C\\[5pt]
C=\frac{100}{2}\\[5pt]
C=50
\end{gather}
\]
L'équation de la vitesse sera
\[
\begin{gather}
\frac{v_x^2}{2}=-{\frac{4x^2}{2}}+50
\end{gather}
\]
en multipliant l'équation par 2 des deux côtés de l'égalité
\[
\begin{gather}
\qquad\quad\quad \frac{v_x^2}{2}=-{\frac{4x^2}{2}}+50 \quad\quad \mathrm{(\times 2)} \\[5pt]
\frac{v_x^2}{\cancel 2}\times \cancel 2=-{\frac{4x^2}{\cancel 2}}\times \cancel 2+50\times 2 \\[5pt]
v_x^2=-4x^2+100
\end{gather}
\]
Quand la vitesse sera égale à zéro, vx = 0, la position sera
\[
\begin{gather}
0^2=-4x^2+100\\[5pt]
4x^2=100\\[5pt]
x=\sqrt{\frac{50}{2}\;}\\[5pt]
x=\sqrt{25\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x=5\;\mathrm m}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .