Solved Problem on Dynamics

A body with a mass of 2 kg and an initial velocity of 10 m/s in the positive direction is under the action of a force that varies with position, given by

\[ \begin{gather} F_x=-8x \qquad\qquad\text{units (SI)} \end{gather} \]

What will be the distance traveled by this body until its velocity becomes zero?

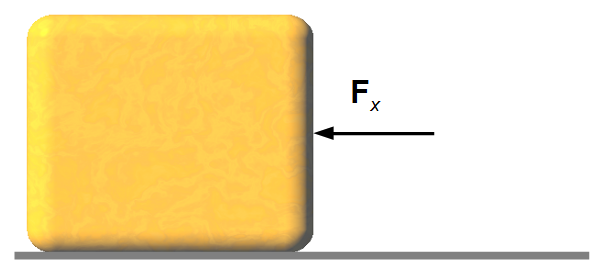
Problem data:

Mass of the body: m = 2 kg;
Initial velocity of the body: v₀ = 10.

Problem diagram:

We choose a reference frame with the x-axis pointed to the right and the y-axis upward (Figure 1).

Figure 1

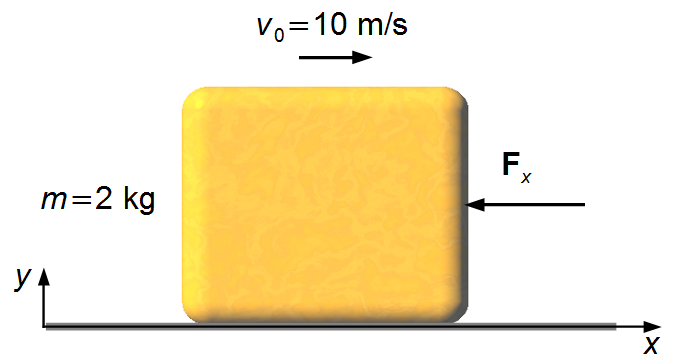
The given force is negative, it is a resistive force that acts in the opposite direction of motion. The force reduces the body's velocity until its final velocity is zero.

Solution:

Applying Newton's Second Law in the x-direction, the given force in the problem is the only force in this direction.

\[ \begin{gather} \bbox[#99CCFF,10px] {\mathbf F=m\frac{d\mathbf v}{dt}} \end{gather} \]

\[ \begin{gather} F_x=m\frac{dv_x}{dt}\\[5pt] -8x=2\frac{dv_x}{dt} \end{gather} \]

multiplying and dividing the right side of the equation by dx

\[ \begin{gather} -4x=\frac{dv_x}{dt}\frac{dx}{dx} \end{gather} \]

reversing the order of the integration terms in the denominator

\[ \begin{gather} -4x=\frac{dv_x}{dx}\frac{dx}{dt} \end{gather} \]

applying the definition of velocity

\[ \begin{gather} \bbox[#99CCFF,10px] {v=\frac{dx}{dt}} \end{gather} \]

integrating in dx on both sides of the equality

\[ \begin{gather} \int -4x\;dx=\int v_x\frac{dv_x}{dx}\;dx\\[5pt] \int-4x\;dx=\int v_x\;dv_x \end{gather} \]

the constant factor (−4) comes out of the integral on the left side

\[ \begin{gather} -4\int x\;dx=\int v_x\;dv_x \end{gather} \]

Integral of \( \displaystyle \int x\;dx \)

\[ \begin{gather} \int x\;dx=\frac{x^{1+1}}{1+1}+C_1=\frac{x^2}{2}+C_1 \end{gather} \]

Integral of \( \displaystyle \int v_x\;dv_x \)

\[ \begin{gather} \int v_x\;dv_x=\frac{v_x^{1+1}}{1+1}+C_2=\frac{v_x^2}{2}+C_2 \end{gather} \]

where C₁ and C₂ are constants of integration.

\[ \begin{gather} -4\left(\frac{x^2}{2}+C_1\right)=\frac{v_x^2}{2}+C_2\\[5pt] -{\frac{4x^2}{2}}-4C_1=\frac{v_x^2}{2}+C_2\\[5pt] -{\frac{4x^2}{2}}-4C_1-C_2=\frac{v_x^2}{2} \end{gather} \]

defining the constants C₁ and C₂ as a new constant C

\[ \begin{gather} C\equiv -4C_1-C_2 \end{gather} \]

The equation for velocity as a function of position will be in the form

\[ \begin{gather} \frac{v_x^2}{2}=-{\frac{4x^2}{2}}+C \end{gather} \]

The constant C is determined using the initial condition given in the problem, at x = 0, and v_x = 10 m/s

\[ \begin{gather} \frac{10^2}{2}=-{\frac{4\times 0^2}{2}}+C\\[5pt] C=\frac{100}{2}\\[5pt] C=50 \end{gather} \]

The equation for velocity will be

\[ \begin{gather} \frac{v_x^2}{2}=-{\frac{4x^2}{2}}+50 \end{gather} \]

multiplying the equation by 2 on both sides of the equality

\[ \begin{gather} \qquad\quad\quad \frac{v_x^2}{2}=-{\frac{4x^2}{2}}+50 \quad\quad \mathrm{(\times 2)} \\[5pt] \frac{v_x^2}{\cancel 2}\times \cancel 2=-{\frac{4x^2}{\cancel 2}}\times \cancel 2+50\times 2 \\[5pt] v_x^2=-4x^2+100 \end{gather} \]

When the velocity is zero, v_x = 0, the position will be

\[ \begin{gather} 0^2=-4x^2+100\\[5pt] 4x^2=100\\[5pt] x=\sqrt{\frac{50}{2}\;}\\[5pt] x=\sqrt{25\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {x=5\;\mathrm m} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .