Exercício Resolvido de Movimento Unidimensional
publicidade
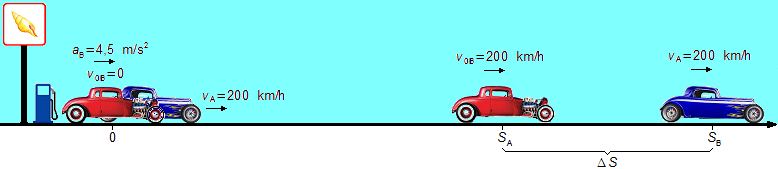
Um carro se desloca por uma estrada retilínea com velocidade constante de 200 km/h. No instante em que este carro passa por um outro carro, inicialmente parado em um posto de gasolina, esse começa a se deslocar com aceleração constante de 4,5 m/s2 até atingir a velocidade de 200 km/h. Determine:
a) Qual é o intervalo de tempo decorrido até que o carro que sai do posto de gasolina atinja a velocidade de 200 km/h?
b) A que distância se encontra um carro do outro quando suas velocidades são iguais.
Dados do problema:
- Velocidade do carro A: vA = 200 km/h;
- Velocidade inicial do carro B: v0B = 0;
- Velocidade final do carro B: vB = 200 km/h;
- Aceleração do carro B: aB = 4,5 m/s2.
Solução
Em primeiro lugar vamos converter as velocidades dos carros dadas em quilômetros por hora (km/h) para metros por segundo (m/s) usado no Sistema Internacional de Unidades (S.I.)
\[
\begin{gather}
v_{\small A}=v_{\small B}=200\frac{\cancel{\mathrm{km}}}{\cancel{\mathrm h}}\times\frac{1000\;\mathrm m}{1\;\cancel{\mathrm{km}}}\times\frac{1\;\cancel{\mathrm h}}{3600\;\mathrm s}=\frac{200}{3,6}\;\frac{\mathrm m}{\mathrm s}=55,6\;\mathrm{m/s}
\end{gather}
\]
a) A função horária da velocidade é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=v_0+a t}
\end{gather}
\]
Para o carro B:
\[
\begin{gather}
v_{\small B}=v_{0 B}+a_{\small B}t\\[5pt]
55,6=0+4,5t\\[5pt]
t=\frac{55,6}{4,5}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\approx 12,4\;\mathrm s}
\end{gather}
\]
b) O carro A se desloca com velocidade constante, está em Movimento Retilíneo Uniforme (M.R.U.), a função horária deste movimento é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+vt}
\end{gather}
\]
aplicando esta equação, usando os dados do carro A e o intervalo de tempo encontrado no item (a)
\[
\begin{gather}
S_{\small A}=S_{0\small A}+v_{\small A}t\\[5pt]
S_{\small A}=0+55,6\times 12,4\\[5pt]
S_{\small A}\approx 689,4\;\mathrm m
\end{gather}
\]
O carro B se desloca com aceleração constante, está em
Movimento Retilíneo Uniformemente Variado (M.R.U.V.), a função horária deste movimento é dada
por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
aplicando esta equação, usando os dados do carro B e o intervalo de tempo encontrado no item (a)
\[
\begin{gather}
S_{\small B}=S_{0\small B}+v_{0\small B}t+\frac{a_{\small B}}{2}t^2\\[5pt]
S_{\small B}=0+0t+\frac{4,5}{2}\times 12,4^2\\[5pt]
S_{\small B}=346\;\mathrm m
\end{gather}
\]
A distância entre os carros será dada por
\[
\begin{gather}
\Delta S=|S_{\small A}-S_{\small B}|\\[5pt]
\Delta S=|689,4-346|
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta S=343,4\;\mathrm m}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .